题目内容
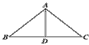
 如图所示,AC是一根垂直于地面的木杆,B是木杆上的一点,且AB=2米,D是地面上一点,AD=3米.在B处有甲、乙两只猴子,D处有一堆食物.甲猴由B往下爬到A处再从地面直奔D处,乙猴则向上爬到木杆顶C处腾空直扑到D处,如果两猴所经过的距离相等,则木杆的长为( )
如图所示,AC是一根垂直于地面的木杆,B是木杆上的一点,且AB=2米,D是地面上一点,AD=3米.在B处有甲、乙两只猴子,D处有一堆食物.甲猴由B往下爬到A处再从地面直奔D处,乙猴则向上爬到木杆顶C处腾空直扑到D处,如果两猴所经过的距离相等,则木杆的长为( )A、
| ||
B、2
| ||
C、3
| ||
| D、5m |
分析:从题意可得到AB+AD=BC+CD(1),AB=2,AD=3,设BC是x,AC=(2+x),DC2=AC2+AD2,把数据代入(1)可得到一元二次方程.
解答:解:设BC的长为x米,
x+
=2+3,
(2+x)2+32=(5-x)2,
x=
,
AC=2+
=2
m.
故选B.
x+
| (2+x)2+32 |
(2+x)2+32=(5-x)2,
x=
| 6 |
| 7 |
AC=2+
| 6 |
| 7 |
| 6 |
| 7 |
故选B.
点评:本题考查了数形结合的思想,通过图形找到等量关系然后列方程求解,本题也复习了勾股定理的运用.

练习册系列答案
相关题目


 m
m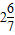 m
m m
m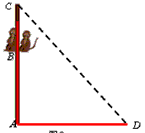
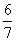 m
m m
m m
m