题目内容
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )

A.  B.
B.  C.
C.  D.
D. 
【答案】A
【解析】分类讨论:当0<x≤1时,根据正方形的面积公式得到y=x2;当1<x≤2时,ED交AB于M,EF交AB于N,利用重叠的面积等于正方形的面积减去等腰直角三角形MNE的面积得到y=x2﹣2(x﹣1)2,配方得到y=﹣(x﹣2)2+2,然后根据二次函数的性质对各选项进行判断.
解:当0<x≤1时,y=x2,
当1<x≤2时,ED交AB于M,EF交AB于N,如图,
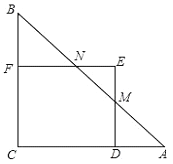
CD=x,则AD=2﹣x,
∵Rt△ABC中,AC=BC=2,
∴△ADM为等腰直角三角形,
∴DM=2﹣x,
∴EM=x﹣(2﹣x)=2x﹣2,
∴S△ENM=![]() (2x﹣2)2=2(x﹣1)2,
(2x﹣2)2=2(x﹣1)2,
∴y=x2﹣2(x﹣1)2=﹣x2+4x﹣2=﹣(x﹣2)2+2,
∴y=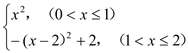 ,
,
故选A.

练习册系列答案
相关题目

