题目内容
【题目】如图,BD=BE,∠D=∠E,∠ABC=∠DBE=90°,BF⊥AE,且点A,C,E在同一条直线上.
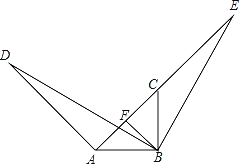
(1)求证:△DAB≌△ECB;
(2)若AD=3,AF=1,求BE的长.
【答案】(1)详见解析;(2)![]()
【解析】
根据角的和差得到∠ABD=∠CBE,利用全等三角形判定即可求解.
根据全等,得到AB=BC,AD=CE,以及等腰三角形性质CF=BF=AF,最后用勾股定理求解.
(1)证明:∵∠ABC=∠DBE=90°,
∴∠ABD=∠CBE,
∵BD=BE,∠D=∠E,
∴△DAB≌△ECB(ASA);
(2)解:∵△DAB≌△ECB;
∴AB=BC,AD=CE,
∵∠ABC=90°,BF⊥AE,
∴CF=BF=AF=1,∠BFE=90°,
∴EF=CF+CE=4,
∴BE=![]() =
=![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?