题目内容
一条直线经过两点A(0,4),B(2,0),如图,将这条直线向左平移与x轴负半轴、y轴负半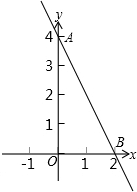 轴分别交于点C、D,使OB=OC.
轴分别交于点C、D,使OB=OC.(1)求证:△DOC≌△AOB;
(2)求直线CD的函数解析式.
分析:(1)根据线段AB向左平移分别与两坐标轴交于点C、D,得到直线CD∥AB,从而得到△DOC≌△AOB;
(2)先求出直线AB的解析式,再根据平移的性质求直线CD的解析式.
(2)先求出直线AB的解析式,再根据平移的性质求直线CD的解析式.
解答: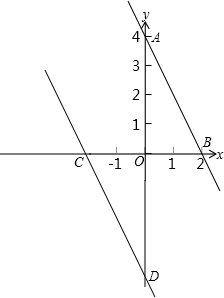 (1)证明:∵将这条直线向左平移与x轴负半轴、y轴负半轴分别交于点C、D,
(1)证明:∵将这条直线向左平移与x轴负半轴、y轴负半轴分别交于点C、D,
∴直线CD∥AB,
∴∠OCD=∠OBA、∠CDO=∠BAO、∈
又OB=OC,
∴△DOC≌△AOB;
(2)解:设直线AB的解析式为y=kx+b,把A(0,4)、点B(2,0)代入得
,
解得
,故直线AB的解析式为y=-2x+4;
∵将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使OB=OC,
∴点C的坐标为(-2,0),
∵平移后的图形与原图形平行,
∴平移以后的函数解析式为:y=-2x+b,
将C(-2,0)代入y=-2x+b,
得b=-4,
∴直线CD的解析式为y=-2x-4.
 (1)证明:∵将这条直线向左平移与x轴负半轴、y轴负半轴分别交于点C、D,
(1)证明:∵将这条直线向左平移与x轴负半轴、y轴负半轴分别交于点C、D,∴直线CD∥AB,
∴∠OCD=∠OBA、∠CDO=∠BAO、∈
又OB=OC,
∴△DOC≌△AOB;
(2)解:设直线AB的解析式为y=kx+b,把A(0,4)、点B(2,0)代入得
|
解得
|
∵将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使OB=OC,
∴点C的坐标为(-2,0),
∵平移后的图形与原图形平行,
∴平移以后的函数解析式为:y=-2x+b,
将C(-2,0)代入y=-2x+b,
得b=-4,
∴直线CD的解析式为y=-2x-4.
点评:本题要注意利用一次函数的特点,列出方程组,求出未知数的值从而求得其解析式,求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
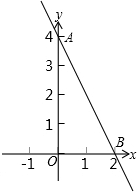 轴分别交于点C、D,使OB=OC.
轴分别交于点C、D,使OB=OC.