题目内容
 28、一条直线经过二次函数y=x2-4x+3图象的顶点A及它与y轴的交点B,求这条直线的解析式,并作出这条直线.
28、一条直线经过二次函数y=x2-4x+3图象的顶点A及它与y轴的交点B,求这条直线的解析式,并作出这条直线.分析:由题意易知,直线过的两点是抛物线的顶点和与y轴的交点,设出函数解析式,把这两点坐标代入即可.
解答:解:由题意得y=x2-4x+3,那么顶点为(2,-1),
当x=0时,y=3,那么与y轴的交点为(0,3).
设直线解析式为y=kx+b,
那么2k+b=-1,b=3,
解得k=-2,
∴直线解析式为y=-2x+3.
如下图,即为直线y=-2x+3的图象.
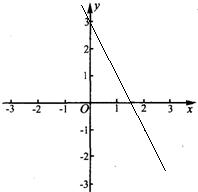
当x=0时,y=3,那么与y轴的交点为(0,3).
设直线解析式为y=kx+b,
那么2k+b=-1,b=3,
解得k=-2,
∴直线解析式为y=-2x+3.
如下图,即为直线y=-2x+3的图象.

点评:本题考查用待定系数法求一次函数解析式,需注意与y轴的交点就是当x=0时,y的值.抛物线的顶点坐标为(-$frac{b}{2a}$,$frac{4ac-{b}^{2}}{4a}$).

练习册系列答案
相关题目
 一条直线经过二次函数y=x2-4x+3图象的顶点A及它与y轴的交点B,求这条直线的解析式,并作出这条直线.
一条直线经过二次函数y=x2-4x+3图象的顶点A及它与y轴的交点B,求这条直线的解析式,并作出这条直线.