题目内容
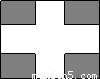
 某中学校园内有一长100m,宽80m的长方形空地,现将其建成花园广场,设计图案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),其余区域为活动区,并且四周出口等宽.若绿化区的总面积恰好占空地面积30%,则每一块矩形绿化区的周长是多少?
某中学校园内有一长100m,宽80m的长方形空地,现将其建成花园广场,设计图案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),其余区域为活动区,并且四周出口等宽.若绿化区的总面积恰好占空地面积30%,则每一块矩形绿化区的周长是多少?
 解:设四周出口宽为x米,则绿化区的长为
解:设四周出口宽为x米,则绿化区的长为 米,宽为
米,宽为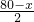 米,
米,根据题意得:4×
 ×
×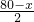 =100×80×30%,
=100×80×30%,整理得:x2-180x+5600=0,
解得:x=140(舍去)或x=40,
故长为
 =30米,宽为
=30米,宽为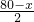 =20米,
=20米,故周长为2×(30+20)=100m.
答:每一块矩形绿化区的周长为100米.
分析:设四周出口宽为x米,则绿化区的长为
 米,宽为
米,宽为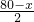 米,根据绿化区的总面积恰好占空地面积30%列出方程求解即可.
米,根据绿化区的总面积恰好占空地面积30%列出方程求解即可.点评:本题考查了一元二次方程的应用,解题关键是设出出口的宽,并用未知数表示出每个矩形的长和宽,从而列出方程.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
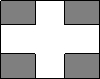 (2012•南漳县模拟)某中学校园内有一长100m,宽80m的长方形空地,现将其建成花园广场,设计图案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),其余区域为活动区,并且四周出口等宽.若绿化区的总面积恰好占空地面积30%,则每一块矩形绿化区的周长是多少?
(2012•南漳县模拟)某中学校园内有一长100m,宽80m的长方形空地,现将其建成花园广场,设计图案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),其余区域为活动区,并且四周出口等宽.若绿化区的总面积恰好占空地面积30%,则每一块矩形绿化区的周长是多少?