题目内容
已知:如图,在正方形ABCD中,AB=4,E为边BC延长线上一点,连接DE,BF⊥DE,垂足为点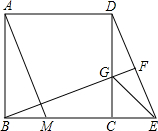 F,BF与边CD交于点G,连接EG.设CE=x.
F,BF与边CD交于点G,连接EG.设CE=x.
(1)求∠CEG的度数;
(2)当BG=2
时,求△AEG的面积;
(3)如果AM⊥BF,AM与BC相交于点M,四边形AMCD的面积为y,求y关于x的函数解析式,并写出它的定义域.
 F,BF与边CD交于点G,连接EG.设CE=x.
F,BF与边CD交于点G,连接EG.设CE=x.(1)求∠CEG的度数;
(2)当BG=2
| 5 |
(3)如果AM⊥BF,AM与BC相交于点M,四边形AMCD的面积为y,求y关于x的函数解析式,并写出它的定义域.
(1)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠DCE=90°.
∵BF⊥DE,
∴∠GFD=90°,
∴∠GBC+∠DGF=90°,∠CDF+∠DGF=90°,
∴∠GBC=∠CDE,
∵∠BGC+∠GBC=90°,∠CDE+∠DEC=90°
∴∠BGC=∠DEC,
在△BCG和△DCE中,
∴△BCG≌△DCE(ASA).
∴GC=EC,即∠CEG=45°.
(2)在Rt△BCG中,BC=4,BG=2
,
利用勾股定理,得CG=2.
∴CE=2,DG=2,即得 BE=6.
∴S△AEG=S四边形ABED-S△ABE-S△ADG-S△DEG
=
(4+6)×4-
×6×4-
×2×4-
×2×2
=2.
(3)由AM⊥BF,BF⊥DE,易得AM∥DE.
于是,由AD∥BC,可知四边形AMED是平行四边形.
∴AD=ME=4.
由CE=x,得MC=4-x.
∴y=S梯形AMCD=
(AD+MC)•CD=
(4+4-x)×4=-2x+16.
即y=-2x+16,定义域为0<x<4.
∴BC=CD,∠BCD=∠DCE=90°.
∵BF⊥DE,

∴∠GFD=90°,
∴∠GBC+∠DGF=90°,∠CDF+∠DGF=90°,
∴∠GBC=∠CDE,
∵∠BGC+∠GBC=90°,∠CDE+∠DEC=90°
∴∠BGC=∠DEC,
在△BCG和△DCE中,
|
∴△BCG≌△DCE(ASA).
∴GC=EC,即∠CEG=45°.
(2)在Rt△BCG中,BC=4,BG=2
| 5 |
利用勾股定理,得CG=2.
∴CE=2,DG=2,即得 BE=6.
∴S△AEG=S四边形ABED-S△ABE-S△ADG-S△DEG
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=2.
(3)由AM⊥BF,BF⊥DE,易得AM∥DE.
于是,由AD∥BC,可知四边形AMED是平行四边形.
∴AD=ME=4.
由CE=x,得MC=4-x.
∴y=S梯形AMCD=
| 1 |
| 2 |
| 1 |
| 2 |
即y=-2x+16,定义域为0<x<4.

练习册系列答案
相关题目