题目内容
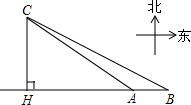 如图,在一笔直的海岸线上有A、B两个观测站,B在A的正东方向,AB=10千米,在某一时刻,从观测站A测得一艘集装箱货船位于北偏西62.6°的C处,同时观测站B测得改集装箱船位于北偏西69.2°方向,问此时该集装箱船与海岸之间距离CH约多少千米?(最后结果保留整数)
如图,在一笔直的海岸线上有A、B两个观测站,B在A的正东方向,AB=10千米,在某一时刻,从观测站A测得一艘集装箱货船位于北偏西62.6°的C处,同时观测站B测得改集装箱船位于北偏西69.2°方向,问此时该集装箱船与海岸之间距离CH约多少千米?(最后结果保留整数)
(参考数据:sin62.6°≈0.89,cos62.6°≈0.46,tan62.6°≈1.93,sin69.2°≈0.93,cos69.2°≈0.36,tan69.2°≈2.63)
解:设CH=x,在直角△ABC中,∠ACH=62.6°,
∵tan∠ACH=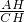 ,
,
∴AH=x•tan62.6°,
在直角△BHC中,∠BCH=69.2°,
∵tan∠BCH= ,
,
∴BH=x•tan69.2°,
∵AB=BH-AH,
∴x•tan69.2°-x•tan62.6°=10,
解得:x=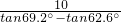 ≈14.
≈14.
答:此时该集装箱船与海岸之间距离CH约14千米.
分析:设CH=x,在直角△ABC中利用三角函数和x,表示出AH的长,同理在直角△BHC中,利用x表示出BH,根据AB=10,即BH-AH=10,即可列方程求得CH的长.
点评:此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.
∵tan∠ACH=
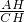 ,
,∴AH=x•tan62.6°,
在直角△BHC中,∠BCH=69.2°,
∵tan∠BCH=
 ,
,∴BH=x•tan69.2°,
∵AB=BH-AH,
∴x•tan69.2°-x•tan62.6°=10,
解得:x=
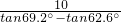 ≈14.
≈14.答:此时该集装箱船与海岸之间距离CH约14千米.
分析:设CH=x,在直角△ABC中利用三角函数和x,表示出AH的长,同理在直角△BHC中,利用x表示出BH,根据AB=10,即BH-AH=10,即可列方程求得CH的长.
点评:此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目