题目内容
如图,扇形OAB的半径OA=6,圆心角∠AOB=90°,C是 上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH=
上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH= DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )
DE.设EC的长为x,△CEH的面积为y,选项中表示y与x的函数关系式的图象可能是( )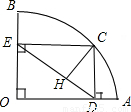
A.
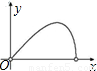
B.
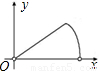
C.
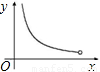
D.
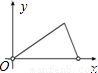
【答案】分析:根据已知得出四边形OACE是矩形,再根据矩形的性质得出DE=OC=6,进而得出EH=4,HD=2,从而得出CE=x,EF= x,表示出FH的长,进而得出△CEH的面积,根据图象得出符合要求的图象.
x,表示出FH的长,进而得出△CEH的面积,根据图象得出符合要求的图象.
解答: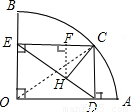 解:连接OC,作HF⊥EC于一点F,
解:连接OC,作HF⊥EC于一点F,
∵扇形OAB的半径OA=6,圆心角∠AOB=90°,CD⊥OA于点D,
CE⊥OB于点E,
∴四边形ODCE是矩形,
∴DE=OC=6,
∵EH= DE,
DE,
∴EH=4,HD=2,
∵CE=x,
∴EF= x,
x,
∴FH=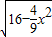 =
=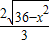 ,
,
∴S△CEH= ×
×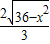 x,
x,
=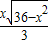 ,
,
A.结合解析式得出只有A图象符合要求;
∵B.图象是一次函数与二次函数一部分,
∴不符合上面解析式,故此选项错误;
∵C.是反比例函数图象,
∴不符合上面解析式,故此选项错误;
∵D.图象是两部分一次函数,
∴不符合上面解析式,故此选项错误.
故选A.
点评:此题主要考查了动点问题的函数图象,得出函数解析式进而得出符合要求的图象是解决问题的关键.
 x,表示出FH的长,进而得出△CEH的面积,根据图象得出符合要求的图象.
x,表示出FH的长,进而得出△CEH的面积,根据图象得出符合要求的图象.解答:
 解:连接OC,作HF⊥EC于一点F,
解:连接OC,作HF⊥EC于一点F,∵扇形OAB的半径OA=6,圆心角∠AOB=90°,CD⊥OA于点D,
CE⊥OB于点E,
∴四边形ODCE是矩形,
∴DE=OC=6,
∵EH=
 DE,
DE,∴EH=4,HD=2,
∵CE=x,
∴EF=
 x,
x,∴FH=
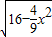 =
=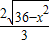 ,
,∴S△CEH=
 ×
×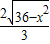 x,
x,=
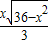 ,
,A.结合解析式得出只有A图象符合要求;
∵B.图象是一次函数与二次函数一部分,
∴不符合上面解析式,故此选项错误;
∵C.是反比例函数图象,
∴不符合上面解析式,故此选项错误;
∵D.图象是两部分一次函数,
∴不符合上面解析式,故此选项错误.
故选A.
点评:此题主要考查了动点问题的函数图象,得出函数解析式进而得出符合要求的图象是解决问题的关键.

练习册系列答案
相关题目
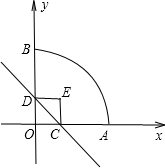 是
是
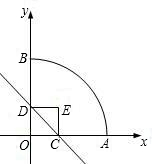 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则: 是______;
是______; 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积. 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.
 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.