题目内容
小明在研究四边形的相关性质时发现,在不改变面积的条件下,一般梯形很难转化为菱形,但有些特殊的梯形通过分割可以转化为菱形.例如以下的等腰梯形就可以转化为菱形(如图1),已知在等腰梯形ABCD中,AD∥BC,AD=10,CD=20,∠C=60°.(1)求梯形ABCD的面积;
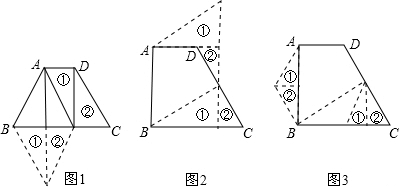
(2)如果将该梯形分割成几块,然后可以重新拼成菱形,试画出变化后的图形(在图1中画出,图形的对应部分标明相同的编号);
(3)在完成上述任务后,他又试着将梯形的形状变为直角梯形(如图2),其它条件不变,将梯形分成几块.
①他能拼成一个菱形吗?如果能,请在图2中画出相应的图形;
②他能拼成一个正六边形吗?如果能,请在图3中画出相应的图形.

分析:(1)因为等腰梯形ABCD中,AD∥BC,AD=10,CD=20,∠C=60°,所以可过D作DE∥CD交于BC于E,因为AD∥BC,所以四边形ABED是平行四边形,所以DE=AB=CD=20,又因∠C=60°,可得△CDE是等边三角形,所以CE=20,BC=10,梯形的高h=10
,然后利用梯形的面积公式即可求解;
(2)能拼成一个菱形,可分别过点A、D作梯形的高,将菱形分割成一个矩形和两个全等的直角三角形,然后再利用矩形的对角线将其分割成两个全等的直角三角形,这四个直角三角形都有一条直角边为10,另一条直角边为梯形的高,即它们都全等,进而以它们的斜边为菱形的边长即可拼接成所求图形;
(3)能拼成菱形,利用直角梯形的与底不垂直的腰的中点E,连接BE,过E作BC的垂线,利用平移和旋转就拼成了一个以AB为边的菱形;能拼成正六边形,利用腰CD的中点E,连接BE,以EC为一边做等边三角形,再作该等边三角形的高,将它分割成三角形①、②,然后将这两个三角形移到A、B处,使A、B处形成120度的角即可解决问题.
| 3 |
(2)能拼成一个菱形,可分别过点A、D作梯形的高,将菱形分割成一个矩形和两个全等的直角三角形,然后再利用矩形的对角线将其分割成两个全等的直角三角形,这四个直角三角形都有一条直角边为10,另一条直角边为梯形的高,即它们都全等,进而以它们的斜边为菱形的边长即可拼接成所求图形;
(3)能拼成菱形,利用直角梯形的与底不垂直的腰的中点E,连接BE,过E作BC的垂线,利用平移和旋转就拼成了一个以AB为边的菱形;能拼成正六边形,利用腰CD的中点E,连接BE,以EC为一边做等边三角形,再作该等边三角形的高,将它分割成三角形①、②,然后将这两个三角形移到A、B处,使A、B处形成120度的角即可解决问题.
解答:解:(1)过D作DE∥AB交于BC于E,
∵AD∥BC,∴四边形ABED是平行四边形,∴DE=AB=CD=20,
∵∠C=60°,∴△CDE是等边三角形,∴CE=20,BC=10,梯形的高h=10
,
∴S梯=
=
=200
;
(2)如图1;
(3)如图2和图3.
∵AD∥BC,∴四边形ABED是平行四边形,∴DE=AB=CD=20,
∵∠C=60°,∴△CDE是等边三角形,∴CE=20,BC=10,梯形的高h=10
| 3 |
∴S梯=
| (AD+BC)h |
| 2 |
(10+30)•10
| ||
| 2 |
| 3 |
(2)如图1;
(3)如图2和图3.

点评:本题一方面考查了学生的动手操作能力,另一方面考查了学生的空间想象能力,重视知识的发生过程,让学生体验学习的过程.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目