题目内容
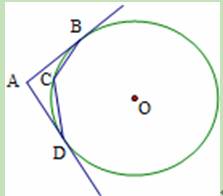
 如图,直线AB、AD与⊙O相切于点B、D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是
如图,直线AB、AD与⊙O相切于点B、D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是
- A.70°
- B.105°
- C.100°
- D.110°
C
分析:过点B作直径BE,连接OD、DE.
根据圆内接四边形性质可求∠E的度数;根据圆周角定理求∠BOD的度数;根据四边形内角和定理求解.
解答: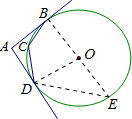 解:过点B作直径BE,连接OD、DE.
解:过点B作直径BE,连接OD、DE.
∵B、C、D、E共圆,∠BCD=140°,
∴∠E=180°-140°=40°.
∴∠BOD=80°.
∵AB、AD与⊙O相切于点B、D,
∴∠OBA=∠ODA=90°.
∴∠A=360°-90°-90°-80°=100°.
故选C.
点评:此题考查了切线的性质、圆内接四边形性质、圆周角定理、四边形内角和定理等知识点,难度中等.
连接切点和圆心是解决有关切线问题时常作的辅助线.
分析:过点B作直径BE,连接OD、DE.
根据圆内接四边形性质可求∠E的度数;根据圆周角定理求∠BOD的度数;根据四边形内角和定理求解.
解答:
 解:过点B作直径BE,连接OD、DE.
解:过点B作直径BE,连接OD、DE.∵B、C、D、E共圆,∠BCD=140°,
∴∠E=180°-140°=40°.
∴∠BOD=80°.
∵AB、AD与⊙O相切于点B、D,
∴∠OBA=∠ODA=90°.
∴∠A=360°-90°-90°-80°=100°.
故选C.
点评:此题考查了切线的性质、圆内接四边形性质、圆周角定理、四边形内角和定理等知识点,难度中等.
连接切点和圆心是解决有关切线问题时常作的辅助线.

练习册系列答案
相关题目
 7、如图,直线AB、AD与⊙O相切于点B、D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是( )
7、如图,直线AB、AD与⊙O相切于点B、D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是( )