题目内容
若方程
的根为正数，则k的取值范围是（ ）| A．k<2 | B．－3<k<2 | C．k≠－3 | D．k<2且 k≠－3 |
A解析:
去分母得，3x+3k=2x+6，解得，x=6-3k，因为方程是正数根，所以6-3k＞0，解得k＜2，则k的取值范围是k＜2．由于分式方程的分母不能为0，即6-3k≠-3，6-3k≠-k∴k≠3，所以k＜2且k≠3，则k＜2．
故选A
去分母得，3x+3k=2x+6，解得，x=6-3k，因为方程是正数根，所以6-3k＞0，解得k＜2，则k的取值范围是k＜2．由于分式方程的分母不能为0，即6-3k≠-3，6-3k≠-k∴k≠3，所以k＜2且k≠3，则k＜2．
故选A
练习册系列答案
相关题目
的根为正数，则k的取值范围是（ ）
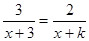的根为正数，则k的取值范围是（ ）
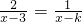的根为正数，则k的取值范围是________．