题目内容
如图，在△MBN中，BM=8，点A、C、D分别在MB、NB、MN上，四边形ABCD为平行四边形，且∠NDC=∠MDA，则四边形ABCD的周长是 ．
【答案】分析：可由平行线及角相等通过转化得出MA=AD，进而可求解四边形的周长．
解答：解：∵四边形ABCD为平行四边形，即AB∥CD，
∴∠M=∠NDC，
又∠NDC=∠MDA，
∴∠M=∠ADM，
∴MA=AD，
四边形ABCD的周长=2（AB+AD）=2（AB+AM）=2×8=16，
故应填16．
点评：本题主要考查平行线的性质及角的转化问题，能够熟练求解．
解答：解：∵四边形ABCD为平行四边形，即AB∥CD，
∴∠M=∠NDC，
又∠NDC=∠MDA，
∴∠M=∠ADM，
∴MA=AD，
四边形ABCD的周长=2（AB+AD）=2（AB+AM）=2×8=16，
故应填16．
点评：本题主要考查平行线的性质及角的转化问题，能够熟练求解．
练习册系列答案
阅读快车系列答案
相关题目
10、如图，在△MBN中，BM=8，点A、C、D分别在MB、NB、MN上，四边形ABCD为平行四边形，且∠NDC=∠MDA，则四边形ABCD的周长是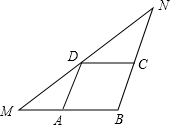
如图，在△MBN中，已知：BM=6，BN=7，MN=10，点A，C，D分别是MB，NB，MN的中点，则四边形ABCD的周长是
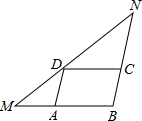如图，在△MBN中，点A、C、D分别在MB、NB、MN上，四边形ABCD为平行四边形，∠NDC=∠MDA，5ND=7DM，平行四边形周长为12，则AB的长为（ ）
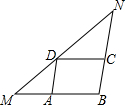（2013•芦淞区模拟）如图，在△MBN中，BM=6，点A，C，D分别在MB，BN，NM上，四边形ABCD为平行四边形，∠NDC=∠MDA，那么平行四边形ABCD的周长是