Question

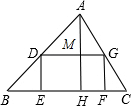如图，有一块三角形土地，它的底边BC=100米，高AH=80米，某单位要沿着地边BC修一座底面是矩形DEFG的大楼，当这座大楼的地基面积最大时．这个矩形的长和宽各是多少？

Answer 1

分析：两三角形相似，对应高之比等于相似比．利用此性质即可解答．

解答：解：∵DG∥BC
∴△ADG∽△ABC
它们的对应高线比等于对应线段的比，
即

AM

AH

=

DG

BC

设AM=x，那么DE=MH=AH-AM=80-x
∴

x

80

=

DG

100

∴DG=

5

4

x
∴S_{四边形DEFG}=DG•DE=（80-x）•

5

4

x=

5

4

（-x²+80x-1600）+

5

4

×1600=-

5

4

（x-40）²+2000
当x=40时，S取最大值
∴DE=40，DG=50
∴矩形的长和宽分别是50m和40m．

点评：此题既要利用相似三角形的性质，又要利用二次函数求最大值，有一定难度．