题目内容
在△ABC中，给出下列各组条件：①∠A：∠B：∠C=3：4：5；②a：b：c=3：4：5；③a=16，b=63，c=65；④a=130，b=128，c=17．其中能判定△ABC是直角三角形的有
- A.1组
- B.2组
- C.3组
- D.4组
B
分析：由直角三角形的定义，只要验证最大角是否是90°；由勾股定理的逆定理，只要验证两小边的平方和是否等于最长边的平方即可．
解答：①∵∠A：∠B：∠C=3：4：5，∴∠C=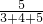
×180°=75°，故不是直角三角形；
B、设a=3k，则b=4k，c=5k，∵（3k）2+（4k）2=（5k）2，故是直角三角形；
C、∵162+632=652，∴能判定△ABC是直角三角形；
D、∵1282+172≠1302，∴不能判定△ABC是直角三角形．
故选B．
点评：本题主要考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
分析：由直角三角形的定义，只要验证最大角是否是90°；由勾股定理的逆定理，只要验证两小边的平方和是否等于最长边的平方即可．
解答：①∵∠A：∠B：∠C=3：4：5，∴∠C=
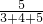×180°=75°，故不是直角三角形；B、设a=3k，则b=4k，c=5k，∵（3k）2+（4k）2=（5k）2，故是直角三角形；
C、∵162+632=652，∴能判定△ABC是直角三角形；
D、∵1282+172≠1302，∴不能判定△ABC是直角三角形．
故选B．
点评：本题主要考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
阅读快车系列答案
相关题目
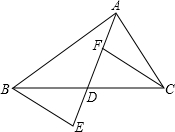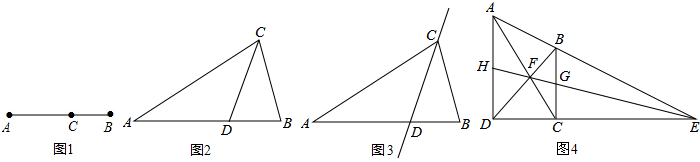
如图，在△ABC中，AB＞AC，D是BC边上的点（不与B，C重合），F，E分别是AD及其延长线上的点，CF∥BE．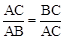
，那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果
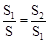，那么称直线l为该图形的黄金分割线.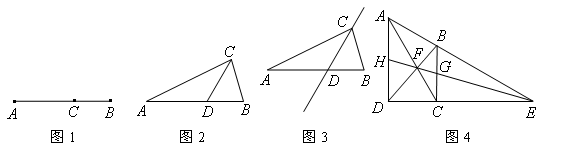
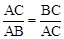，那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果
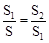，那么称直线l为该图形的黄金分割线.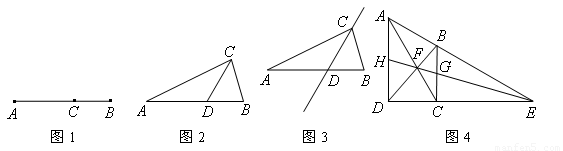
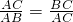，那么称点C为线段AB的黄金分割点．某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果
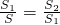，那么称直线l为该图形的黄金分割线．