题目内容
 已知:抛物线
已知:抛物线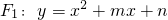 的顶点为A(1,0)
的顶点为A(1,0)
(1)求F1的函数解析式;
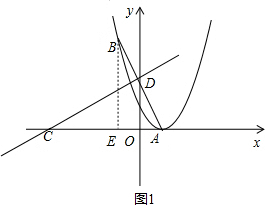
(2)如图,直线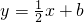 交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线
交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线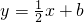 对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式;
对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式;
(3)将(2)中求得的抛物线F2向左平移n个单位得抛物线F3,抛物线F3的顶点为点P,是否存在n使得tan∠BAP= ?若存在试求n的值;若不存在,请说明理由.
?若存在试求n的值;若不存在,请说明理由.
 解:(1)设F1的函数解析式为y=(x-h)2+k,
解:(1)设F1的函数解析式为y=(x-h)2+k,∵抛物线
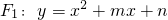 的顶点为A(1,0)
的顶点为A(1,0)∴y=(x-1)2+0
即F1的解析式为:
 ;
;(2)如图,设直线
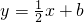 交x轴于点C,交y轴于点D,那么CD垂直平分AB.
交x轴于点C,交y轴于点D,那么CD垂直平分AB.当y=0时,x=-2b,即C(-2b,0).
当x=0时,y=b,即D(0,b).
则OC=2b,OD=b.
易证△ABE∽△CDO,故
 =
= ,
,∴BE=2AE,
∴直线AB为y=-2x+2,

∴根据题意得:

解得:
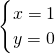 (不合题意,舍去)或
(不合题意,舍去)或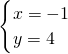
∴点B的坐标为(-1,4).
∵抛物线F2的顶点为点B,
∴设F2的函数解析式为y=a(x+1)2+4.
又∵抛物线F2经过点A(1,0),
∴F2的函数解析式为0=a(1+1)2+4,
解得:a=-1,
∴


(3)存在n使得tan∠BAP=
 .理由如下:
.理由如下:如图3,过点B作BF⊥AP于点F,过点F作直线FG⊥x轴于点G,交BP于点H.
易证△BHF∽△FGA,则
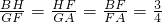 ,又FG+FH=4,AG-BH=2,故可求得F
,又FG+FH=4,AG-BH=2,故可求得F ,
,故直线AF的解析式为
 ,
,又由于点P的纵坐标为4,故P(-7,4),得n=6.
分析:(1)设F1的函数解析式为y=(x-h)2+k,然后将顶点坐标代入即可求解;
(2)设直线
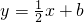 交x轴于点C,交y轴于点D,那么CD垂直平分AB,不难证明△ABE∽△CDO,由于OC=2b,OD=b,故BE=2AE,可求得直线AB为y=-2x+2,与F1联立可求得点B的坐标为(-1,4),故可得抛物线的解析式;
交x轴于点C,交y轴于点D,那么CD垂直平分AB,不难证明△ABE∽△CDO,由于OC=2b,OD=b,故BE=2AE,可求得直线AB为y=-2x+2,与F1联立可求得点B的坐标为(-1,4),故可得抛物线的解析式;(3)如图,过点B作BF⊥AC于点F,过点F作FD⊥x轴于点D,过点B作BE⊥DF于点E,易证△BEF∽△FDA,则
 ,又FE+FD=4,AD-BE=2,故可求得F
,又FE+FD=4,AD-BE=2,故可求得F ,故直线AF的解析式为
,故直线AF的解析式为 ,又由于点P的纵坐标为4,故P(-7,4),得n=6.
,又由于点P的纵坐标为4,故P(-7,4),得n=6.点评:本题考查了二次函数综合题.此题涉及到的知识点有:待定系数法求二次函数、一次函数解析式,相似三角形的判定与性质,平移的性质等.解答(3)题,注意构造相似三角形的辅助线的作法.

练习册系列答案
相关题目
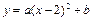
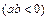 的顶点为A,与x轴的交点为B,C(点B
的顶点为A,与x轴的交点为B,C(点B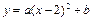
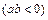 的顶点为A,与x轴的交点为B,C(点B
的顶点为A,与x轴的交点为B,C(点B 的顶点为A(1,0)
的顶点为A(1,0) 交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线
交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线 对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式;
对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式; ?若存在试求n的值;若不存在,请说明理由.
?若存在试求n的值;若不存在,请说明理由.