题目内容
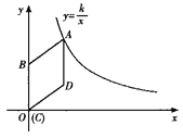
【题目】如图，直线y＝k1x＋7(k1＜0)与x轴交于点A，与y轴交于点B，与反比例函数y＝
(k2＞0)在第一象限的图象交于C，D两点，点O为坐标原点，△AOB的面积为
，点C的横坐标为1.
(1)求反比例函数的解析式；
(2)如果一个点的横、纵坐标都是整数，那么我们就称这个点为“整点”，请求出图中阴影部分(不含边界)所包含的所有整点的坐标．
【答案】(1) y＝－x＋7. y＝
.(2) (2，4)，(3，3)，(4，2)．
【解析】（1）分别令x=0、y=0，求得对应y和x的值，从而的得到点A、B的坐标，然后依据三角形的面积公式可求得k1的值，然后由直线的解析式可求得点C的坐标，由点C的坐标可求得反比例函数的解析式；
（2）由函数的对称性可求得D（6，1），从而可求得x的值范围，然后求得当x=2、3、4、5时，一次函数和反比例函数对应的函数值，从而可得到整点的坐标．
（1）∵当x=0时，y=7，当y=0时，x=-
，
∴A（-，0）、B（0、7）．
∴S△AOB=
|OA||OB|=×（-）×7=
，解得k1=-1．
∴直线的解析式为y=-x+7．
∵当x=1时，y=-1+7=6，
∴C（1，6）．
∴k2=1×6=6．
∴反比例函数的解析式为y=．
（2）∵点C与点D关于y=x对称，
∴D（6，1）．
当x=2时，反比例函数图象上的点为（2，3），直线上的点为（2，5），此时可得整点为（2，4）；
当x=3时，反比例函数图象上的点为（3，2），直线上的点为（3，4），此时可得整点为（3，3）；
当x=4时，反比例函数图象上的点为（4，
），直线上的点为（4，3），此时可得整点为（4，2）；
当x=5时，反比例函数图象上的点为（5，
），直线上的点为（5，2），此时，不存在整点．
综上所述，符合条件的整点有（2，4）、（3，3）、（4，2）．
