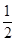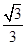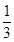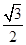题目内容
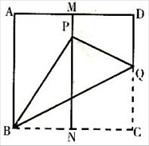
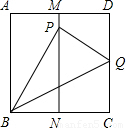
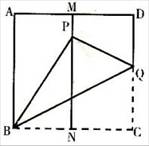
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
A、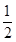 B、
B、 C、
C、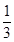 D、
D、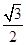
【答案】
B
【解析】
试题分析:由折叠的性质知∠BPQ=∠C=90°,利用直角三角形中的cos∠PBN=BN:PB=1:2,可求得∠PBN=60°,∠PBQ=30°,从而可以求得结果.
∵∠CBQ=∠PBQ=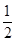 ∠PBC,BC=PB=2BN=1,∠BPQ=∠C=90°
∠PBC,BC=PB=2BN=1,∠BPQ=∠C=90°
∴cos∠PBN=BN:PB=1:2
∴∠PBN=60°,∠PBQ=30°
∴PQ=PBtan30°=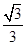
故选B.
考点:本题考查的是折叠的性质,正方形的性质,直角三角形的性质,锐角三角函数的概念
点评:解答本题的关键是熟练掌握折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
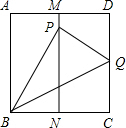 如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD、BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连接PQ,则PQ=
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD、BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连接PQ,则PQ=