题目内容

小华同学学习了第二十五章《锐角三角比》后，对求三角形的面积方法进行了研究，得到了新的结论：
（1）如图1，已知锐角△ABC．求证： $数学公式$ ；
（2）根据题（1）得到的信息，请完成下题：如图2，在等腰△ABC中，AB=AC=12厘米，点P从A点出发，沿着边AB移动，点Q从C点出发沿着边CA移动，点Q的速度是1厘米/秒，点P的速度是点Q速度的2倍，若它们同时出发，设移动时间为t秒，
问：当t为何值时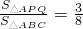， $数学公式$ ？

解：（1）如图1，
过点C作CE⊥AB于点E，
sinA= $\text{[math]}$ ，
∴EC=ACsinA，
S_△ABC= $\text{[math]}$ EC×AB= $\text{[math]}$ AB×ACsinA；

（2）如图2，过点P作PE⊥AC于点E，过点B作BF⊥AC于点F，
设移动时间为t秒，则AP=2t，CQ=t，
∴PE=APsinA，BF=12sinA，
S_△APQ= $\text{[math]}$ AQ×PE= $\text{[math]}$ ×（12-t）×APsinA= $\text{[math]}$ ×（12-t）×2t×sinA=t（12-t）sinA，
S_△ABC= $\text{[math]}$ BF×AC= $\text{[math]}$ ×12×12sinA=72sinA，
当 $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ ，
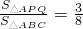∴整理得出：t²-12t+27=0，
解得：t₁=3，t₂=9（不合题意舍去），
∴当t为3时， $\text{[math]}$ ．
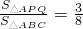分析：（1）首先过点C作CE⊥AB于点E，则sinA= $\text{[math]}$ ，进而得出EC的长，即可得出答案；
（2）首先表示出△APQ的面积，进而得出△ABC的面积，进而利用 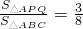$\text{[math]}$ 求出t的值即可．
点评：此题主要考查了解直角三角形的应用和一元二次方程的解法，根据已知表示出△APQ的面积是解题关键．