题目内容
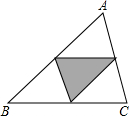 学校美化一个三角形空地ABC,如图所示,计划把各边中点连线所围成的三角形区域内种上花,其余部分铺成草坪,那么种花的面积与草坪的面积之比是
学校美化一个三角形空地ABC,如图所示,计划把各边中点连线所围成的三角形区域内种上花,其余部分铺成草坪,那么种花的面积与草坪的面积之比是
- A.1:4
- B.4:1
- C.1:3
- D.3:4
A
分析:利用三角形的中位线定理,可以得到两个三角形的对应边的比相等,根据三边的比对应相等的三角形相似即可证得两个三角形,再根据相似三角形的面积的比等于相似比的平方即可求解.
解答: 解:∵D,E分别是AB,AC的中点,
解:∵D,E分别是AB,AC的中点,
∴DE= BC,
BC,
即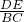 =
= ,
,
同理,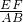 =
= ,
,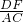 =
= ,
,
∴ =
= ,
,
∴△FED∽△ABC,且相似比是 .
.
∴面积的比是:( )2=1:4.
)2=1:4.
故选A.
点评:本题考查了三角形的中位线定理,以及相似三角形的判定与性质,正确证明两个三角形的对应边的比相等是关键.
分析:利用三角形的中位线定理,可以得到两个三角形的对应边的比相等,根据三边的比对应相等的三角形相似即可证得两个三角形,再根据相似三角形的面积的比等于相似比的平方即可求解.
解答:
 解:∵D,E分别是AB,AC的中点,
解:∵D,E分别是AB,AC的中点,∴DE=
 BC,
BC,即
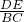 =
= ,
,同理,
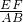 =
= ,
,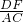 =
= ,
,∴
 =
= ,
,∴△FED∽△ABC,且相似比是
 .
.∴面积的比是:(
 )2=1:4.
)2=1:4.故选A.
点评:本题考查了三角形的中位线定理,以及相似三角形的判定与性质,正确证明两个三角形的对应边的比相等是关键.

练习册系列答案
相关题目
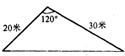 学校校园内有一块如图所示的三角形空地,计划将这块空地建成一个花园,以美化校园环境.预计花园每平方米造价为30元,学校建这个花园需要投资
学校校园内有一块如图所示的三角形空地,计划将这块空地建成一个花园,以美化校园环境.预计花园每平方米造价为30元,学校建这个花园需要投资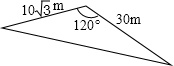 学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园,以美化环境,预计花园每平方米造价为30元,学校建这个花园至少需要投资
学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园,以美化环境,预计花园每平方米造价为30元,学校建这个花园至少需要投资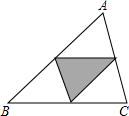 学校美化一个三角形空地ABC,如图所示,计划把各边中点连线所围成的三角形区域内种上花,其余部分铺成草坪,那么种花的面积与草坪的面积之比是( )
学校美化一个三角形空地ABC,如图所示,计划把各边中点连线所围成的三角形区域内种上花,其余部分铺成草坪,那么种花的面积与草坪的面积之比是( )