Question

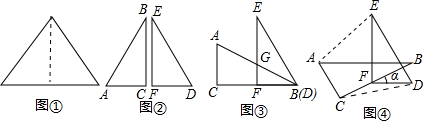
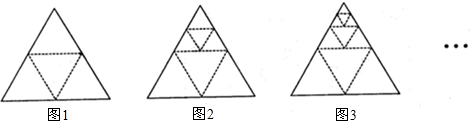
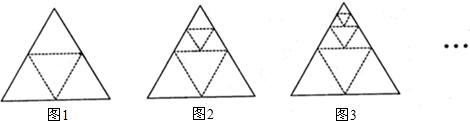
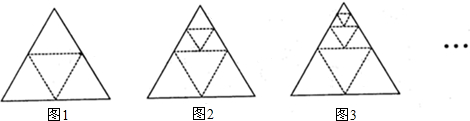
如图所示，将一个等边三角形各边中点连接起来，得到四个小等边三角形（如图1），再将最上边的一个小等边三角形按同样的方法画出四个更小的等边三角形（如图2），然后再按同样地方法画出第三个图形（如图3）…如此继续下去，第n个图中有________个等边三角形．（用含n的式子表示）

Answer 1

（4n+1）
分析：分析数据可得：图1中等边三角形的个数是1+3+1=5；图2中等边三角形的个数是5+3+1=9；图3中等边三角形的个数是9+3+1=13个，依此类推，可得到第n个图中等边三角形的个数．
解答：∵图1中等边三角形的个数是5=4×1+1；
图2中等边三角形的个数是9=4×2+1；
图3个图中等边三角形的个数是13=4×3+1；
…
∴第n个图中有（4n+1）个等边三角形．
故答案为（4n+1）．
点评：本题考查了图形的变化类，是一道寻找规律的题目，对于这种类型的题目可以采用由特殊到一般的归纳方法．