��Ŀ����
����Ŀ����ijһ�������������¶��壺���ں���y������![]() ������ֵy����
������ֵy����![]() ��������
��������![]() ����ƴ˺���Ϊ��k���ͺϺ�����
����ƴ˺���Ϊ��k���ͺϺ�����
���磺����������![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ����ã�
����ã�![]() �����Ժ���
�����Ժ���![]() Ϊ��3���ͺϺ�����.
Ϊ��3���ͺϺ�����.
��1����һ�κ���![]() Ϊ��k���ͺϺ���������k��ֵΪ______��
Ϊ��k���ͺϺ���������k��ֵΪ______��
����һ�κ���![]() Ϊ��1���ͺϺ���������a��ֵ��
Ϊ��1���ͺϺ���������a��ֵ��
��2������������![]() ��
��![]() ��
��![]() ��
��![]() ���ǡ�k���ͺϺ���������
���ǡ�k���ͺϺ���������![]() �������
�������![]() ��ֵ��
��ֵ��
��3����֪���κ���![]() ����
����![]() ʱ��y�ǡ�k���ͺϺ���������k��ȡֵ��Χ.
ʱ��y�ǡ�k���ͺϺ���������k��ȡֵ��Χ.
���𰸡���1����2����![]() ����2��2018����3����a��1ʱ��
����2��2018����3����a��1ʱ��![]() ����0��a��1ʱ��
����0��a��1ʱ��![]() ������1��a��0ʱ��
������1��a��0ʱ��![]() ����a����1ʱ��
����a����1ʱ��![]() .
.
��������
��1���ٸ�����k���ͺϺ������Ķ��弴�����k��ֵ��
�ڸ���a��ȡֵ��Χ�������ۣ�Ȼ���ٸ�����1���ͺϺ������Ķ���ֱ���a��ֵ���ɣ�
��2�����ݷ����������������ԣ����y��ȡֵ��Χ��Ȼ�������k���ͺϺ������Ķ��弴�����ab��ֵ��Ȼ��������ȫƽ����ʽ�ı��μ������![]() ��ֵ��
��ֵ��
��3�����ݶԳ�����x��ȡֵ��Χ�����λ�÷������ۣ���i����a��1ʱ����![]() �ڶԳ�����࣬���ݶ��κ��������������y��ȡֵ��Χ��Ȼ�������k���ͺϺ������Ķ��弴�����k��a�Ĺ�ϵ������a��ȡֵ���k��ȡֵ���ɣ���ii����0��a��1ʱ����
�ڶԳ�����࣬���ݶ��κ��������������y��ȡֵ��Χ��Ȼ�������k���ͺϺ������Ķ��弴�����k��a�Ĺ�ϵ������a��ȡֵ���k��ȡֵ���ɣ���ii����0��a��1ʱ����![]() ���Գ��ᣬ��x=��1��Գ�����Զ��ԭ��ͬ�ϣ���iii������1��a��0ʱ����
���Գ��ᣬ��x=��1��Գ�����Զ��ԭ��ͬ�ϣ���iii������1��a��0ʱ����![]() ���Գ��ᣬ��x=1��Գ�����Զ��ԭ��ͬ�ϣ���iiii����a����1ʱ����
���Գ��ᣬ��x=1��Գ�����Զ��ԭ��ͬ�ϣ���iiii����a����1ʱ����![]() �ڶԳ����Ҳ࣬ԭ��ͬ��.
�ڶԳ����Ҳ࣬ԭ��ͬ��.
�⣺��1���١�һ�κ���![]() ��
��![]() ʱ
ʱ![]() ��
��
������k���ͺϺ������Ķ��壺![]() ��
��
��ã�k=2��
�ڵ�a��0ʱ��
��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
������1���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ��
��
��a��0ʱ��
��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
������1���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ��
��
����������![]() ��
��
��2����![]() ��
��![]() ��
��![]() ��
��![]() ����
����
�൱![]() ʱ��y��x���������С��
ʱ��y��x���������С��
��![]() ��
��
������k���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ��
��
��![]() ��
��
��![]() ��
��
��3�����κ���![]() �ĶԳ���Ϊ��
�ĶԳ���Ϊ��![]() ��
��
��i����a��1ʱ����![]() �ڶԳ�����࣬����ͼ��ʾ��
�ڶԳ�����࣬����ͼ��ʾ��
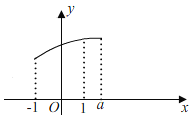
���ѷ��֣���x=1ʱ��y���ֵΪ��![]() ��
��
��x=��1ʱ��y��СֵΪ��![]() ��
��
������k���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ��
��
��a��1��
��![]() ��
��
��ii����0��a��1ʱ����![]() ���Գ��ᣬ��x=��1��Գ�����Զ������ͼ��ʾ��
���Գ��ᣬ��x=��1��Գ�����Զ������ͼ��ʾ��
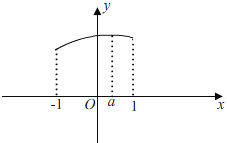
���ѷ��֣���x=aʱ��y���ֵΪ��![]() ��
��
��x=��1ʱ��y��СֵΪ��![]() ��
��
������k���ͺϺ������Ķ��壺![]() ��
��
��ã�![]() ���˺����ĶԳ���Ϊ��a=��1���������ϣ�
���˺����ĶԳ���Ϊ��a=��1���������ϣ�
��0��a��1�ڶԳ�����Ҳ࣬k��a�����������
�൱0��a��1ʱ����ã�![]() ��
��
��iii������1��a��0ʱ����![]() ���Գ��ᣬ��x=1��Գ�����Զ������ͼ��ʾ��
���Գ��ᣬ��x=1��Գ�����Զ������ͼ��ʾ��
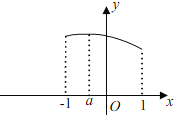
���ѷ��֣���x=aʱ��y���ֵΪ��![]() ��
��
��x=1ʱ��y��СֵΪ��![]() ��
��
������k���ͺϺ������Ķ��壺![]()
��ã�![]() ���˺����ĶԳ���Ϊ��a=1���������ϣ�
���˺����ĶԳ���Ϊ��a=1���������ϣ�
�ੁ1��a��0�ڶԳ������࣬k��a���������С
�൱��1��a��0ʱ����ã�![]() ��
��
��iiii����a����1ʱ����![]() �ڶԳ����Ҳ࣬����ͼ��ʾ��
�ڶԳ����Ҳ࣬����ͼ��ʾ��

���ѷ��֣���x=1ʱ��y��СֵΪ��![]() ��
��
��x=��1ʱ��y���ֵΪ��![]() ��
��
������k���ͺϺ������Ķ��壺![]()
��ã�![]()
��a����1��
��![]() ��
��
������������a��1ʱ��![]() ����0��a��1ʱ��
����0��a��1ʱ��![]() ������1��a��0ʱ��
������1��a��0ʱ��![]() ����a����1ʱ��
����a����1ʱ��![]() .
.