题目内容
矩形ABCD中,对角线AC、BD交于点O,∠BOC=2∠DOC,若AC=8cm,则AD长为
- A.4cm
- B.8cm
- C.
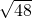 cm
cm - D.
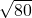 cm
cm
C
分析:由∠BOC=2∠DOC,可知∠DOC=60°,再由矩形的性质得OC=OD,从而得∠ODC=∠OCD,则△OCD为等边三角形,所以CD=4cm,然后根据勾股定理即可求出AD.
解答:∵∠BOC=2∠DOC
∵∠BOC+∠DOC=180°
∴∠DOC=60°
∵矩形ABCD
∴OC=OD=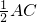 =4cm
=4cm
∴∠ODC=∠OCD
∴△OCD为等边三角形
∴CD=OC=OD=4cm
∴AD=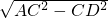 =
=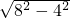 =
=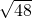 cm
cm
故选C.
点评:利用矩形的性质和已知条件,推出△OCD为等边三角形是解题的关键,这样就可知道CD的长,然后根据勾股定理求解.
分析:由∠BOC=2∠DOC,可知∠DOC=60°,再由矩形的性质得OC=OD,从而得∠ODC=∠OCD,则△OCD为等边三角形,所以CD=4cm,然后根据勾股定理即可求出AD.
解答:∵∠BOC=2∠DOC
∵∠BOC+∠DOC=180°
∴∠DOC=60°
∵矩形ABCD
∴OC=OD=
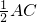 =4cm
=4cm∴∠ODC=∠OCD
∴△OCD为等边三角形
∴CD=OC=OD=4cm
∴AD=
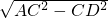 =
=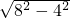 =
=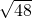 cm
cm故选C.
点评:利用矩形的性质和已知条件,推出△OCD为等边三角形是解题的关键,这样就可知道CD的长,然后根据勾股定理求解.

练习册系列答案
相关题目
 =∠DCE.
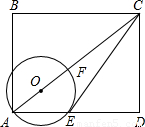
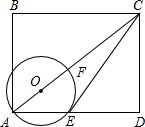
=∠DCE.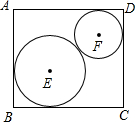 如图,矩形ABCD中,AB=8,BC=9,⊙E和⊙F相外切,且它们分别与矩形的一对对角的两边相切,则圆心距EF=
如图,矩形ABCD中,AB=8,BC=9,⊙E和⊙F相外切,且它们分别与矩形的一对对角的两边相切,则圆心距EF=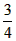 ,AE=7,求⊙O的直径。
,AE=7,求⊙O的直径。
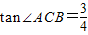 ,AE=7,求⊙O的直径.
,AE=7,求⊙O的直径.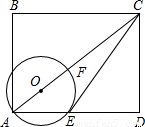
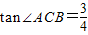 ,AE=7,求⊙O的直径.
,AE=7,求⊙O的直径.