题目内容
如图,要设计一个矩形的花坛,花坛长60m,宽40m,有两条纵向甬道和一条横向甬道,横向甬道的两侧有两个半圆环形甬道,半圆环形甬道的内半圆的半径为10m,横向甬道的宽度是其它各甬道宽度的2倍.设横向甬道的宽为2x m.(π的值取3)(1)用含x的式子表示两个半圆环形甬道的面积之和;
(2)当所有甬道的面积之和比矩形面积的
 多36m2时,求x的值;
多36m2时,求x的值;(3)根据设计的要求,x的值不能超过3m.如果修建甬道的总费用(万元)与x(m)成正比例关系,比例系数是7.59,花坛其余部分的绿化费用为0.03万元/m2,那么x为何值时,所建花坛的总费用最少?最少费用是多少万元?
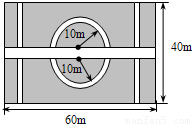
【答案】分析:(1)由于半圆环形甬道的内半圆的半径为10m,横向甬道的宽度是其它各甬道宽度的2倍,而横向甬道的宽为2x,由此得到半圆环形甬道的外半圆的半径为(10+x)m,然后利用圆的面积公式即可求出两个半圆环形甬道的面积之和;
(2)首先用x表示所有甬道的面积之和为40×x×2+60×2x-2x2×2+3x2+60x,然后根据已知条件的关于x的方程,解方程即可求解;
(3)由于修建甬道的总费用(万元)与x(m)成正比例关系,比例系数是7.59,因此得到修建甬道的总费用为7.59x,而花坛其余部分的绿化费用为0.03万元/m2,花坛其余部分的面积为[60×40-(-x2+260x)],因此即可求出所建花坛的总费用y与x的函数关系式,然后利用二次函数的性质即可求出所建花坛的最少费用.
解答:解:(1)两个半圆环形甬道的面积=π(10+x)2-π×102=3x2+60x(m2);
(2)依题意,得40×x×2+60×2x-2x2×2+3x2+60x= ×60×40+36,
×60×40+36,
整理,得x2-260x+516=0,
解得x1=2,x2=258(不符合题意,舍去).
∴x=2;
(3)设建设花坛的总费用为y万元,则
y=0.03×[60×40-(-x2+260x)]+7.59x
=0.03x2-0.21x+72.
∴当x=- =
=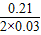 =3.5时,y的值最小.
=3.5时,y的值最小.
因为根据设计的要求,x的值不能超过3,
∴当x=3时,总费用最少.
最少费用为y=0.03×32-0.21×3+72=71.64(万元).
点评:本题考查了二次函数的性质在实际生活中的应用.最大(小)值的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x= 时取得.
时取得.
(2)首先用x表示所有甬道的面积之和为40×x×2+60×2x-2x2×2+3x2+60x,然后根据已知条件的关于x的方程,解方程即可求解;
(3)由于修建甬道的总费用(万元)与x(m)成正比例关系,比例系数是7.59,因此得到修建甬道的总费用为7.59x,而花坛其余部分的绿化费用为0.03万元/m2,花坛其余部分的面积为[60×40-(-x2+260x)],因此即可求出所建花坛的总费用y与x的函数关系式,然后利用二次函数的性质即可求出所建花坛的最少费用.
解答:解:(1)两个半圆环形甬道的面积=π(10+x)2-π×102=3x2+60x(m2);
(2)依题意,得40×x×2+60×2x-2x2×2+3x2+60x=
 ×60×40+36,
×60×40+36,整理,得x2-260x+516=0,
解得x1=2,x2=258(不符合题意,舍去).
∴x=2;
(3)设建设花坛的总费用为y万元,则
y=0.03×[60×40-(-x2+260x)]+7.59x
=0.03x2-0.21x+72.
∴当x=-
 =
=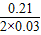 =3.5时,y的值最小.
=3.5时,y的值最小.因为根据设计的要求,x的值不能超过3,
∴当x=3时,总费用最少.
最少费用为y=0.03×32-0.21×3+72=71.64(万元).
点评:本题考查了二次函数的性质在实际生活中的应用.最大(小)值的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=
 时取得.
时取得. 
练习册系列答案
相关题目
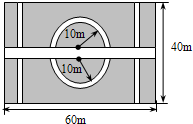 横向甬道的宽度是其它各甬道宽度的2倍.设横向甬道的宽为2x m.(π的值取3)
横向甬道的宽度是其它各甬道宽度的2倍.设横向甬道的宽为2x m.(π的值取3)
 多36 m2时,求x的值.
多36 m2时,求x的值. 多36m2时,求x的值;
多36m2时,求x的值;