题目内容
如图,某小区有一个长为40m,宽为26m的矩形场地,计划修建一横两纵的三条同样宽度的小路,其余部分种草,若使分割的每一块草坪的面积都为144m2,求小路的宽度.
【答案】分析:本题中草坪的总面积=矩形场地的面积-三条道路的面积和+三条道路中重叠的两个小正方形的面积,据此可得出关于道路宽度的方程,求出道路的宽度.
解答:解:设小路的宽为x米,则(40-2x)(26-x)=6×144,
整理得,x2-46x+88=0,解得:x1=2,x2=44,
∵x2=44超过矩形的边长,
∴x2=44不合题意,
符合题意的是x=2
答:小路的宽为2m
点评:本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
解答:解:设小路的宽为x米,则(40-2x)(26-x)=6×144,
整理得,x2-46x+88=0,解得:x1=2,x2=44,
∵x2=44超过矩形的边长,
∴x2=44不合题意,
符合题意的是x=2
答:小路的宽为2m
点评:本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,某小区有一个等腰梯形的场地,上底长120m,下底长200m,上下底相距80m,在两腰中点连线处有一条东西方向横向大道,南门有两条纵向大道,宽度与横向大道等宽,北门有一条纵向大道,宽为横向大道的2倍.大道的所有面积占梯形面积的19%,问东西方向大道的宽应是多少米?
如图,某小区有一个等腰梯形的场地,上底长120m,下底长200m,上下底相距80m,在两腰中点连线处有一条东西方向横向大道,南门有两条纵向大道,宽度与横向大道等宽,北门有一条纵向大道,宽为横向大道的2倍.大道的所有面积占梯形面积的19%,问东西方向大道的宽应是多少米? 如图,某小区有一个长为40m,宽为26m的矩形场地,计划修建一横两纵的三条同样宽度的小路,其余部分种草,若使分割的每一块草坪的面积都为144m2,求小路的宽度.
如图,某小区有一个长为40m,宽为26m的矩形场地,计划修建一横两纵的三条同样宽度的小路,其余部分种草,若使分割的每一块草坪的面积都为144m2,求小路的宽度. 如图,某小区有一个长为40m,宽为26m的矩形场地,计划修建一横两纵的三条同样宽度的小路,其余部分种草,若使分割的每一块草坪的面积都为144m2,求小路的宽度.
如图,某小区有一个长为40m,宽为26m的矩形场地,计划修建一横两纵的三条同样宽度的小路,其余部分种草,若使分割的每一块草坪的面积都为144m2,求小路的宽度.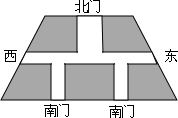 如图,某小区有一个等腰梯形的场地,上底长120m,下底长200m,上下底相距80m,在两腰中点连线处有一条东西方向横向大道,南门有两条纵向大道,宽度与横向大道等宽,北门有一条纵向大道,宽为横向大道的2倍.大道的所有面积占梯形面积的19%,问东西方向大道的宽应是多少米?
如图,某小区有一个等腰梯形的场地,上底长120m,下底长200m,上下底相距80m,在两腰中点连线处有一条东西方向横向大道,南门有两条纵向大道,宽度与横向大道等宽,北门有一条纵向大道,宽为横向大道的2倍.大道的所有面积占梯形面积的19%,问东西方向大道的宽应是多少米?