题目内容
已知，如图，一轮船在离A港10千米的P地出发，向B港匀速行驶．30分钟后离港26千米（未到达B港前），设出发x小时后，轮船离A港y千米（未到达B港前）．则 y与x的函数关系式为（ ）
A．y=
B．y=26
C．y=32x-10
D．y=32x+10
【答案】分析：根据轮船的速度=（26-10）÷0.5=32千米/时，轮船离A港距离=10+行驶距离得出．
解答：解：∵一轮船在离A港10千米的P地出发，向B港匀速行驶．30分钟后离港26千米（未到达B港前），
∴轮船的速度=（26-10）÷0.5=32（千米/时），
则依题意有：y=32x+10．
故选：D．
点评：此题主要考查了由实际问题抽象出一次函数关系式，求出轮船的速度是解决本题的关键．
解答：解：∵一轮船在离A港10千米的P地出发，向B港匀速行驶．30分钟后离港26千米（未到达B港前），
∴轮船的速度=（26-10）÷0.5=32（千米/时），
则依题意有：y=32x+10．
故选：D．
点评：此题主要考查了由实际问题抽象出一次函数关系式，求出轮船的速度是解决本题的关键．
练习册系列答案
相关题目
9、已知，如图，一轮船在离A港10千米的P地出发向家B港匀速前进，30分钟后离A港26千米（未到达B港）．设出发x小时后，轮船离A港y千米（未到达B港），则y与x之间的函数关系是y=
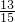x