题目内容
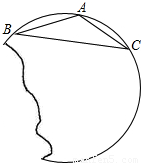
 如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
(1)试确定 所在圆的圆心O;
所在圆的圆心O;
(2)设△ABC是等腰三角形,底边BC=10厘米,腰AB=6厘米,求圆片的半径R.(结果保留根号)
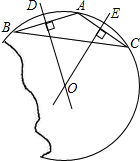
解:(1)作DO⊥AB.DO必过圆心,作EO⊥AC,EO必过圆心,DO、EO交点必为圆心;
(2)
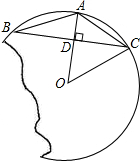
设半径为r.连接OA,因为BA=AC,故AO⊥BC.
所以:CD= ×10=5,AD=
×10=5,AD= =
= .
.
根据勾股定理,(R- )2+52=R2,解得R=
)2+52=R2,解得R=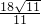 .
.
分析:(1)根据垂径定理,作DO⊥AB.DO必过圆心,作EO⊥AC,EO必过圆心,DO、EO交点必为圆心;
(2)连接AO.根据AB=AC,AO过圆心,依据垂径定理推论,可判断AO⊥BC,根据勾股定理求半径.
点评:此题是一道实际问题,将圆的相关知识和勾股定理结合,有一定的开放性,可以作出图形,根据勾股定理和垂径定理解答.

(2)

设半径为r.连接OA,因为BA=AC,故AO⊥BC.
所以:CD=
 ×10=5,AD=
×10=5,AD= =
= .
.根据勾股定理,(R-
 )2+52=R2,解得R=
)2+52=R2,解得R=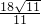 .
.分析:(1)根据垂径定理,作DO⊥AB.DO必过圆心,作EO⊥AC,EO必过圆心,DO、EO交点必为圆心;
(2)连接AO.根据AB=AC,AO过圆心,依据垂径定理推论,可判断AO⊥BC,根据勾股定理求半径.
点评:此题是一道实际问题,将圆的相关知识和勾股定理结合,有一定的开放性,可以作出图形,根据勾股定理和垂径定理解答.

练习册系列答案
相关题目
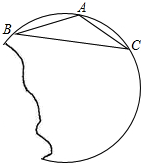 如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
如图,要把破残的圆片复制完整,已知弧上的点A、B、C.
 如图,要把破残的圆片复制完整,已知弧上的三点A、B、C,
如图,要把破残的圆片复制完整,已知弧上的三点A、B、C,
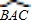 所在圆的圆心O;
所在圆的圆心O;