题目内容
【题目】小明将两个全等的等腰三角板摆放在一起,其中∠ACB=∠DFE=90°,AB=DE=12.
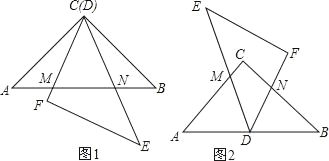
(1)如图1,当D与C点重合时,CF、CE分别与AB交于M、N两点,且量得AM=3,BN=4,小明发现AM、MN、BN存在某种数量关系,他想:当AM=a,BN=b,MN=c时,这种数量关系仍成立吗?请你一起探究并证明这个结论;
(2)如图2,当等腰Rt△DEF的顶点D恰好在AB的中点处时,DE、DF分别与AC、BC交于M、N,小明经测量后猜想,AMBN是一个定值.你认可他的猜想吗?说明理由,若猜想成立,请求出该定值.
(3)在(2)的条件下,△DEF绕点D旋转,DE、DF所在的直线分别交线段AC和线段BC于点M、N,若CN=2![]() ,求MN的长.
,求MN的长.
【答案】(1)猜想:当AM=a,BN=b,MN=c时,有a2+b2=c2.,证明详见解析;(2)小明的猜想正确,理由详见解析;(3)MN的长为![]() .
.
【解析】
(1)由小明量得的数据可猜想当AM=a,BN=b,MN=c时,有a2+b2=c2.可过点B作BG⊥AB,并使得BG=AM,连接CG、GN,从而将AM、NB归结到Rt△NBG中,只需证MN=GN,只需证△MCN≌△GCN,只需证∠MCN=∠NCG,CM=CG,只需证△AMC≌△BGC即可.
(2)由∠A=∠EDF=∠B=45°可证△AMD∽△BDN,根据相似三角形的性质可得AMBN=ADBD=36,从而解决问题.
(3)由条件可求出CA、CB的长,然后由CN可求出BN,再借用(2)中的结论可求出AM,从而可求出CM,在Rt△MCN中运用勾股定理就可解决问题.
解:(1)∵AM=3,BN=4,AB=12,
∴MN=AB﹣AM﹣BN=12﹣3﹣4=5,
∴AM2+BN2=MN2.
猜想:当AM=a,BN=b,MN=c时,有a2+b2=c2.
理由如下:
过点B作BG⊥AB,并使得BG=AM,连接CG、GN,如图1,
则有∠ABG=90°.
∵∠ABC=45°,
∴∠GBC=45°.
在△AMC和△BGC中,
 ,
,
∴△AMC≌△BGC(SAS),
∴CM=CG,∠ACM=∠BCG,
∴∠MCG=∠ACB=90°.
∵∠MCN=45°,
∴∠NCG=∠MCG﹣∠MCN=45°,
∴∠MCN=∠NCG.
在△MCN和△GCN中,
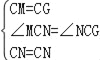 ,
,
∴△MCN≌△GCN(SAS),
∴MN=GN.
在Rt△NBG中,
∵∠NBG=90°,
∴BN2+BG2=GN2,
∴BN2+AM2=MN2.
(2)小明的猜想正确.
理由如下:
如图2,
由题可得∠A=∠MDN=∠B=45°,
∵∠MDB=∠A+∠AMD=∠MDN+∠NDB,
∴∠AMD=∠NDB,
∴△AMD∽△BDN,
∴![]() =
=![]() ,
,
∴AMBN=ADBD.
∵D为AB的中点,AB=12,
∴AD=BD=6,
∴AMBN=36.
∴AMBN是一个定值,该定值为36.
(3)连接MN,如图3,
在Rt△ACB中,
∵∠C=90°,AC=BC,AB=12,
∴AC=BC=6![]() .
.
![]() ,∴BN=4
,∴BN=4![]() .
.
∵AMBN=36.
∴AM=![]() ,
,
∴CM=CA﹣AM=6![]() ﹣
﹣![]() =
=![]() .
.
在Rt△MCN中,
∵∠C=90°,
∴MN2=CM2+CN2=(![]() )2+(2
)2+(2![]() )2
)2
=.![]() +8=
+8=![]() ,
,
∴MN=![]() .
.
∴MN的长为![]() .
.