题目内容
已知:如图,BC是圆O的弦,线段AD经过圆心O,点A在圆上,AD⊥BC,垂足为点D ,
,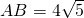 ,
,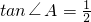 .
.
(1)弦BC的长;
(2)圆O半径的长.
解:(1)∵AD⊥BC,tanA= ,
,
∴BD= AD,
AD,
∵AB=4 ,BD2+AD2=AB2,
,BD2+AD2=AB2,
∴BD=4,AD=8,
又∵经过圆心O的直线AD⊥BC,
∴BC=2BD=8;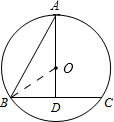
(2)连接OB.设圆O的半径为r,那么DO=8-r,
在△BOD中,(8-r)2+42=r2,
∴r=5,
即圆O的半径为5.
分析:(1)利用勾股定理及所给的正切值可得BD的长,乘以2即为弦BC的长;
(2)连接OB,构造出以OC为斜边的直角三角形,利用勾股定理即可求得半径长.
点评:本题综合考查了垂径定理,勾股定理及解直角三角形的知识;利用题中的直角三角形求解是解决本题的关键.
 ,
,∴BD=
 AD,
AD,∵AB=4
 ,BD2+AD2=AB2,
,BD2+AD2=AB2,∴BD=4,AD=8,
又∵经过圆心O的直线AD⊥BC,
∴BC=2BD=8;

(2)连接OB.设圆O的半径为r,那么DO=8-r,
在△BOD中,(8-r)2+42=r2,
∴r=5,
即圆O的半径为5.
分析:(1)利用勾股定理及所给的正切值可得BD的长,乘以2即为弦BC的长;
(2)连接OB,构造出以OC为斜边的直角三角形,利用勾股定理即可求得半径长.
点评:本题综合考查了垂径定理,勾股定理及解直角三角形的知识;利用题中的直角三角形求解是解决本题的关键.

练习册系列答案
相关题目
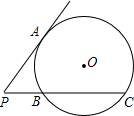 已知:如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=2PB,求
已知:如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=2PB,求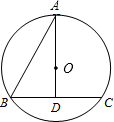 ,
, ,
, .
.
 ,
, .
.