题目内容
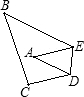 把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠AEB+∠ADC之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是
把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠AEB+∠ADC之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是
- A.∠A=∠AEB+∠ADC
- B.2∠A=∠AEB+∠ADC
- C.3∠A=2∠AEB+∠ADC
- D.3∠A=2(∠AEB+∠ADC)
B
分析:由已知条件,根据三角形内角和定理得到∠1+∠3=∠B+∠C=180°-∠A,即可求解.
解答: 解:
解:
∵∠1=∠2,∠3=∠4,且∠1+∠3+∠A=180°
∴∠1+∠2+∠3+∠4=360°-2∠A.
∵∠1+∠2+∠3+∠4=2×180°-∠AEB-∠ADC
∴2∠A=∠AEB+∠ADC
故选B.
点评:本题考查了轴对称的性质、三角形内角和定理及三角形外角的性质;作为一个选择题,可以利用特殊的三角形来确定选项,利用特殊图形是解决一些选择题的有效方法.
分析:由已知条件,根据三角形内角和定理得到∠1+∠3=∠B+∠C=180°-∠A,即可求解.
解答:
 解:
解:∵∠1=∠2,∠3=∠4,且∠1+∠3+∠A=180°
∴∠1+∠2+∠3+∠4=360°-2∠A.
∵∠1+∠2+∠3+∠4=2×180°-∠AEB-∠ADC
∴2∠A=∠AEB+∠ADC
故选B.
点评:本题考查了轴对称的性质、三角形内角和定理及三角形外角的性质;作为一个选择题,可以利用特殊的三角形来确定选项,利用特殊图形是解决一些选择题的有效方法.

练习册系列答案
相关题目
 7、把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠AEB+∠ADC之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
7、把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠AEB+∠ADC之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ) 20、如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE的内部,则( )
20、如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE的内部,则( ) 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内时,则∠A与∠1+∠2之间的数量关系是:
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内时,则∠A与∠1+∠2之间的数量关系是: 把△ABC纸片沿DE折叠,点A落在四边形BCDE的外部,已知∠1=100°,∠2=40°求∠A的度数.
把△ABC纸片沿DE折叠,点A落在四边形BCDE的外部,已知∠1=100°,∠2=40°求∠A的度数.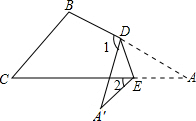 如图,△ABC中,∠A=20°,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠1和∠2的数量关系正确的是( )
如图,△ABC中,∠A=20°,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠1和∠2的数量关系正确的是( )