题目内容
在圆内接四边形ABCD中,则∠A:∠B:∠C=2:3:4,则∠D的度数是( )
| A、60° | B、90° |
| C、1 20° | D、30° |
考点:圆内接四边形的性质
专题:
分析:可设∠A=2x,则∠B=3x,∠C=4x;利用圆内接四边形的对角互补,可求出∠A、∠C的度数,进而求出∠B和∠D的度数,由此得解.
解答:解:∵∠A:∠B:∠C=2:3:4,
∴设∠A=2x,则∠B=3x,∠C=4x,
∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,即2x+4x=180,解得x=30°,
∴∠B=3x=90°,
∴∠D=180°-∠B=180°-90°=90°,
故选B.
∴设∠A=2x,则∠B=3x,∠C=4x,
∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,即2x+4x=180,解得x=30°,
∴∠B=3x=90°,
∴∠D=180°-∠B=180°-90°=90°,
故选B.
点评:本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在正方形网格中,△ABC的位置如图,则sinB的值是( )
在正方形网格中,△ABC的位置如图,则sinB的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
有一个商店把某件商品按进价加20%作为定价,可是总卖不出去;后来老板按定价降价20%以96元出售,则这件商品的进价为( )
| A、100元 | B、96元 |
| C、86元 | D、70元 |
下列计算,结果正确的是( )
| A、a2•a3=a5 |
| B、(x-y)2=x2-y2 |
| C、x2y3÷2x2y=2y2 |
| D、(-3a2)3=-9a6 |
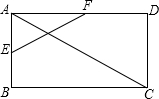 如图,矩形ABCD中,E、F分别是AB、AD的中点,已知AB=6,AF=4,则AC=
如图,矩形ABCD中,E、F分别是AB、AD的中点,已知AB=6,AF=4,则AC=