题目内容
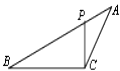
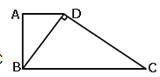
【题目】如图，在梯形ABCD中，AD∥BC，∠BAD=90°，对角线BD⊥DC, 如果AD=4，BC=9，则BD的长=___________ 。
【答案】6
【解析】
观察图形,根据AD∥BC,利用平行线的性质可知∠ADB=∠CBD,结合已知条件,
由∠BAD=90°，对角线BD⊥DC,可知∠BAD=∠BDC,根据两角对应相等的两个三角形相似,即可得到△ABD∽△DCB;利用相似三角形的性质,可得
，即可求解.
∵ AD∥BC
∴ ∠ADB=∠CBD (两直线平行,内错角相等)
∵ ∠BAD=90° ,BD⊥DC,
∴ ∠BAD=∠BDC=90°,
∵ ∠ADB=∠CBD ∠BAD=∠BDC,
∴ △ABD∽△DCB (两角对应相等的两个三角形相似)
∴(相似三角形的三边对应成比例)
∴
∵AD=4，BC=9
∴BD=6
故答案为：6.
练习册系列答案
阅读快车系列答案
相关题目
