题目内容
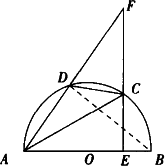
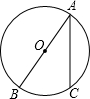如图，AB是⊙O的直径，AC是弦，∠BAC=30°，则
的度数是
- A.30°
- B.60°
- C.90°
- D.120°
D
分析：先连接BC，根据直径所对的圆周角是直角，再利用直角三角形两锐角互余求解即可．
解答：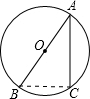
解：连接BC．
∵AB是⊙O的直径，
∴∠C=90°，
∴∠ABC=90°-30°=60°，
∴的度数是120°．
故选D．
点评：本题主要考查了圆周角定理．熟练运用圆周角定理的推论以及直角三角形的两个锐角互余的性质是解题的关键．
分析：先连接BC，根据直径所对的圆周角是直角，再利用直角三角形两锐角互余求解即可．
解答：
解：连接BC．∵AB是⊙O的直径，
∴∠C=90°，
∴∠ABC=90°-30°=60°，
∴
的度数是120°．故选D．
点评：本题主要考查了圆周角定理．熟练运用圆周角定理的推论以及直角三角形的两个锐角互余的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
8、如图，AB是铅直地竖立在坡角为30°的山坡上的电线杆，当阳光与水平线成60°角时，电线杆的影子BC的长度为4米，则电线杆AB的高度为（ ）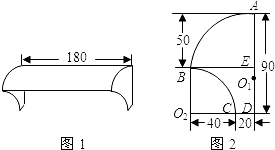
0.1平方米）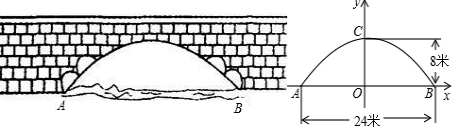
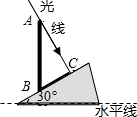如图，AB是铅直地竖立在坡角为30°的山坡上的电线杆，当阳光与水平线成60°角时，电线杆的影子BC的长度为4米，则电线杆AB的高度为