题目内容
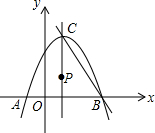 如图,已知抛物线
如图,已知抛物线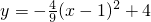 ,与x轴交于A、B两点,点C为抛物线的顶点.点P在抛物线的对称轴上,设⊙P的半径为r,当⊙P与x轴和直线BC都相切时,则圆心P的坐标为________.
,与x轴交于A、B两点,点C为抛物线的顶点.点P在抛物线的对称轴上,设⊙P的半径为r,当⊙P与x轴和直线BC都相切时,则圆心P的坐标为________.
 或(1,-6)
或(1,-6)分析:设P点坐标为(1,a),求出B和C点的坐标,进而求出直线BC的解析式,再求出点P到直线BC的距离,根据⊙P与x轴和直线BC都相切,列出等式求出a的值.
解答:设P点坐标为(1,a),
∵抛物线的解析式为
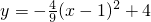 ,
,∴抛物线顶点C的坐标为(1,4),
令y=0,解得B点的坐标为(4,0),
设直线BC的解析式为y=kx+b,
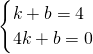 ,
,解得k=-
 ,b=
,b=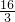 ,
,则直线BC的解析式为y=-
 x+
x+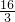 ,
,点P到直线BC的距离d=
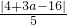 ,
,点P到x轴的距离为|a|,
又知⊙P与x轴和直线BC都相切时,
即
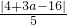 =|a|,
=|a|,解得a=
 或a=-6.
或a=-6.故P点的坐标为
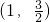 或(1,-6).
或(1,-6).故答案为
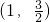 或(1,-6).
或(1,-6).点评:本题主要考查二次函数的综合题的知识点,解答本题的关键是熟练运用点到直线的距离公式,此题难度不大.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
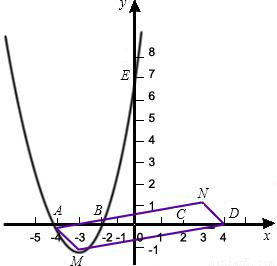
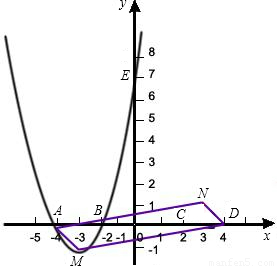
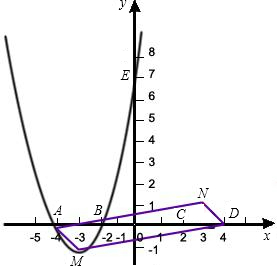 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).