题目内容
如图,某公园入口处原有三级台阶,每级台阶高为20cm,深为30cm,为方便残疾人士,拟将台阶改成斜坡,高台阶的起点为A,斜坡的起始点为C(如图所示),现将斜坡的坡角∠BCA设计为12°,那么斜坡起点C应离A点多远?
(精确到1cm,sin12°=0.208,cos12°=0.978,tan12°=0.213)
(精确到1cm,sin12°=0.208,cos12°=0.978,tan12°=0.213)

分析:首先过点B作BD⊥AC于点D,由题意得:BD=20×3=60(cm),AD=30×2=60(cm),∠C=12°,然后由三角函数的性质,求得CD的长,继而求得答案.
解答: 解:过点B作BD⊥AC于点D,
解:过点B作BD⊥AC于点D,
由题意得:BD=20×3=60(cm),AD=30×2=60(cm),∠C=12°,
在Rt△BCD中,CD=
=
≈282(cm)
∴AC=CD-AD=222(cm).
答:斜坡起点C应离A点约222cm.
 解:过点B作BD⊥AC于点D,
解:过点B作BD⊥AC于点D,由题意得:BD=20×3=60(cm),AD=30×2=60(cm),∠C=12°,
在Rt△BCD中,CD=
| BD |
| tan12° |
| 60 |
| 0.213 |
∴AC=CD-AD=222(cm).
答:斜坡起点C应离A点约222cm.
点评:此题考查了坡度坡角问题.此题难度不大,注意构造直角三角形,并借助与直角三角形的性质求解是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 16、如图,某公园入口处原有三阶台阶,每级台阶高为20cm,深为30cm.为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现将斜坡的坡度设计为i=1:4.5,则AC的长为
16、如图,某公园入口处原有三阶台阶,每级台阶高为20cm,深为30cm.为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现将斜坡的坡度设计为i=1:4.5,则AC的长为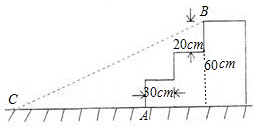

 ,则AC的长度是 cm.
,则AC的长度是 cm.
