题目内容
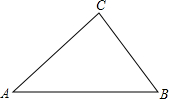
已知：如图，在△ABC中，AB=8，AC=9，∠A=48°．
求：（1）AB边上的高（精确到0.01）；
（2）∠B的度数（精确到1′）．
求：（1）AB边上的高（精确到0.01）；
（2）∠B的度数（精确到1′）．
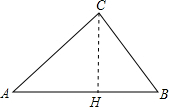
（1）作AB边上的高CH，垂足为H，
∵在Rt△ACH中，sinA=
，
∴CH=AC•sinA=9sin48°≈6.69；
（2）∵在Rt△ACH中，cosA=
，
∴AH=AC•cosA=9cos48°，
∴在Rt△BCH中，tanB=
=
=
≈3.382，
∴∠B≈73°32′．
∵在Rt△ACH中，sinA=
| CH |
| AC |
∴CH=AC•sinA=9sin48°≈6.69；
（2）∵在Rt△ACH中，cosA=
| AH |
| AC |
∴AH=AC•cosA=9cos48°，
∴在Rt△BCH中，tanB=
| CH |
| BH |
| CH |
| AB-AH |
| 9sin48° |
| 8-9cos48° |
∴∠B≈73°32′．
练习册系列答案
名校课堂系列答案
相关题目
显示的结果是（ ）
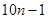个选手各对局一次，计分方式为：胜者的2分，负者得0分，平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍，则n的所有可能值是 .