题目内容
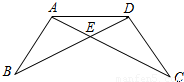
 在一次数学课上,王老师在黑板上画出一幅图,如图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.
在一次数学课上,王老师在黑板上画出一幅图,如图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两作为条件,来证明AE=DE.请写出所以可能的情况用序号表示),并选其中的一种加以证明.
分析:根据对顶角相等可得∠AEB=∠DEC,再根据全等三角形的判定方法,选出△ABE和△DCE全等的条件即可得解.
解答:解:可能情况有:①③、②③、①④、②④.
选择①AB=DC,③∠B=∠C证明.
在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AE=DE.
选择①AB=DC,③∠B=∠C证明.
在△ABE和△DCE中,
|
∴△ABE≌△DCE(AAS),
∴AE=DE.
点评:本题考查了全等三角形的判定与性质,确定出所要证明的两条相等的线段所在的三角形以及由图形可知的条件是解题的关键,注意所选条件不能满足“边边角”.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
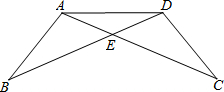
 在一次数学课上,王老师在黑板上画出图,如图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推出△AED是等腰三角形.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)
在一次数学课上,王老师在黑板上画出图,如图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推出△AED是等腰三角形.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)