题目内容
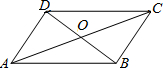 如图,OA=OC,OB=OD,则图中全等三角形共有
如图,OA=OC,OB=OD,则图中全等三角形共有
- A.2对
- B.3对
- C.4对
- D.5对
C
分析:根据SAS可证明△AOB≌△COD,△AOD≌△BOC,则∠BAC=∠DCA,∠CAD=∠BCA,AB=CD,AD=BC,利用SSS可证明△ABC≌△CDA,△ABD≌△BDC.
解答:∵OA=OC,OB=OD,∠AOB=∠COD,∠AOD=∠BOC,
∴△AOB≌△COD,△AOD≌△BOC,
∴∠BAC=∠DCA,∠CAD=∠BCA,AB=CD,AD=BC,
∴△ABC≌△CDA,△ABD≌△BDC.
故选C.
点评:本题考查了全等三角形的判定,注意:要证明两个三角形全等,至少要有一条边.
分析:根据SAS可证明△AOB≌△COD,△AOD≌△BOC,则∠BAC=∠DCA,∠CAD=∠BCA,AB=CD,AD=BC,利用SSS可证明△ABC≌△CDA,△ABD≌△BDC.
解答:∵OA=OC,OB=OD,∠AOB=∠COD,∠AOD=∠BOC,
∴△AOB≌△COD,△AOD≌△BOC,
∴∠BAC=∠DCA,∠CAD=∠BCA,AB=CD,AD=BC,
∴△ABC≌△CDA,△ABD≌△BDC.
故选C.
点评:本题考查了全等三角形的判定,注意:要证明两个三角形全等,至少要有一条边.

练习册系列答案
相关题目


 9、如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( )
9、如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( )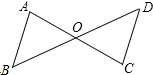 已知:如图,OA=OC,OB=OD,试说明:△AOB≌△COD.
已知:如图,OA=OC,OB=OD,试说明:△AOB≌△COD. 8、如图,OA=OC,OB=OD,则图中全等三角形共有
8、如图,OA=OC,OB=OD,则图中全等三角形共有 10、如图,OA⊥OC,OB⊥OD,∠BOC=35°,则∠AOD=
10、如图,OA⊥OC,OB⊥OD,∠BOC=35°,则∠AOD=