题目内容
(2013•廊坊一模)一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色不同外其余都相同),其中有2个白球,1个黄球.若从中任意摸出一个球,这个球是白球的概率是
,则口袋中红球有
| 1 | 3 |
3
3
个.分析:首先假设红球为x个,再让白球的个数除以球的总个数即为白球的概率
,进而得出红球的个数即可.
| 1 |
| 3 |
解答:解:∵一个不透明的口袋里装有红、白、黄三种颜色的乒乓球,2个白球,1个黄球,从中任意摸出一个球,这个球是白球的概率是
,
∴设口袋中有红球x个,则
=
,
解得:x=3,
∴则口袋中红球有3个.
故答案为:3.
| 1 |
| 3 |
∴设口袋中有红球x个,则
| 2 |
| x+2+1 |
| 1 |
| 3 |
解得:x=3,
∴则口袋中红球有3个.
故答案为:3.
点评:此题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
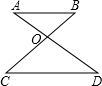 (2013•廊坊一模)如图,AB∥CD,AD,BC相交于O,∠BAD=42°,∠BOD=83°,则∠C的度数是( )
(2013•廊坊一模)如图,AB∥CD,AD,BC相交于O,∠BAD=42°,∠BOD=83°,则∠C的度数是( )