题目内容
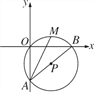
【题目】如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.
(1)求⊙P的半径及圆心P的坐标;
(2)M为劣弧OB的中点,求证:AM是∠OAB的平分线.
【答案】(1)5,P(4,-3).(2)证明见解析
【解析】分析:(1)先利用勾股定理计算出AB=10,再利用圆周角定理的推理可判断AB为 P的直径,则得到 P的半径是5,然后利用线段的中点坐标公式得到P点坐标;
(2)根据圆周角定理由弧OM=弧BM,,∠OAM=∠MAB,于是可判断AM为∠OAB的平分线;
本题解析:
(1)解:∵O(0,0),A(0,-6),B(8,0),∴OA=6,OB=8,∴AB=![]() =10.∵∠AOB=90°,∴AB为⊙P的直径,∴⊙P的半径是5.∵点P为AB的中点,∴P(4,-3).
=10.∵∠AOB=90°,∴AB为⊙P的直径,∴⊙P的半径是5.∵点P为AB的中点,∴P(4,-3).
(2)证明:∵M点是劣弧OB的中点,∴弧OM=弧BM,∴∠OAM=∠MAB,∴AM为∠OAB的平分线.

练习册系列答案
相关题目
