题目内容
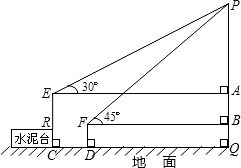 如图,广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲、乙二人分别从E、F处看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.8米,请问此气球离地面的高度是多少?(结果保留到0.1米,参考数据:
如图,广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲、乙二人分别从E、F处看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.8米,请问此气球离地面的高度是多少?(结果保留到0.1米,参考数据:| 3 |
分析:由于气球的高度为PA+AB+FD,而AB=1米,FD=0.8米,可设PA=h米,根据题意,列出关于h的方程可求解.
解答:解:设PA=x(米),
∵∠PFB=45°,
∴BF=PB=1+x,
∴EA=x+6,
在Rt△PEA中,
∵PA=AEtan30°,
∴x=(x+6)tan30°,3x=(x+6)
,
∴x=
=
=
≈8.2(米),
∴PA+AB+FD=8.2+1+0.8=10.0(米).
答:该气球的高度为10.0米.
∵∠PFB=45°,
∴BF=PB=1+x,
∴EA=x+6,
在Rt△PEA中,
∵PA=AEtan30°,
∴x=(x+6)tan30°,3x=(x+6)
| 3 |
∴x=
6
| ||
3-
|
| 6 | ||
|
6(
| ||
| 2 |
∴PA+AB+FD=8.2+1+0.8=10.0(米).
答:该气球的高度为10.0米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 如图,数轴上有一个等边△AOC,点O与原点重合,点A与表示-5的点重合,△AOC经过平移或轴对称或旋转都可以得到△OBD.
如图,数轴上有一个等边△AOC,点O与原点重合,点A与表示-5的点重合,△AOC经过平移或轴对称或旋转都可以得到△OBD.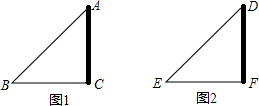 如图,广场上有两根旗杆,都垂直于地面放置.已知太阳光线AB与DE是平行的,经过测量这两根旗杆在太阳光下的影子一样长,那么这两根旗杆的高度相等吗?说说你的理由.
如图,广场上有两根旗杆,都垂直于地面放置.已知太阳光线AB与DE是平行的,经过测量这两根旗杆在太阳光下的影子一样长,那么这两根旗杆的高度相等吗?说说你的理由.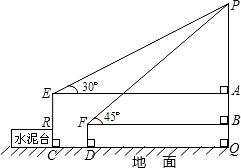 如图,广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲、乙二人分别从E、F处看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.8米,请问此气球离地面的高度是多少?(结果保留到0.1米,参考数据:
如图,广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲、乙二人分别从E、F处看气球的仰角分别是30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.8米,请问此气球离地面的高度是多少?(结果保留到0.1米,参考数据: )
)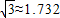 )
)