Question

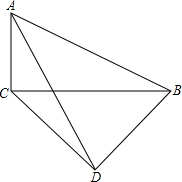我市某校初三年级数学课外兴趣小组的同学们对手上的两块三角板进行了探索，他们发现：将两块三角板按如图放置，连接AD，能确定cot∠CAD的值，你认为cot∠CAD=

 

．

Answer 1

分析：根据三角板的特殊角和特殊的边长关系表示出要求的边的邻边与对边，然后求解即可．

解答：解：作DE⊥BC于E点，
设AC=a，则BC=

3

a，DC=DB=

6

2

a，DE=

3

2

a，
∵AC∥DE
∴

AC

DE

=

CF

EF

设CF=x，则EF=

3

2

a-x
∴

a

3 2 a

=

x

3 2 a-x

解得：x=（2

3

-3）a
∴cot∠CAD=

AC

CF

=

a

(2 3 -3)a

=

2 3

3

+1．
故答案为

2 3

3

+1．

点评：本题考查了解直角三角形的知识，解题的关键是正确的表示出要求角的邻边与对边．