题目内容
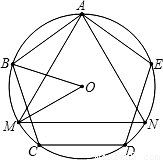
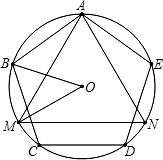如图，正三角形AMN与正五边形ABCDE内接于⊙O，则∠BOM的度数是________．
48°
分析：连接AO，根据正三角形AMN与正五边形ABCDE内接于⊙O，分别求出∠AOM和∠AOB的度数，然后两角相减即为∠BOM的度数
解答：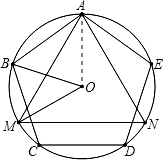
解；
连接AO，
∵正三角形AMN与正五边形ABCDE内接于⊙O，
∴∠AOM=
×360°=120°，
∴∠AOB=
×360°=72°，
∵∠BOM=∠AOM-∠AOB，
∴∠BOM=120°-72°=48°
故答案为：48°
点评：本题主要考查正多边形和圆这一知识点，解答此题的关键是连接AO，由等弧所对的圆心角相等来解决问题．
分析：连接AO，根据正三角形AMN与正五边形ABCDE内接于⊙O，分别求出∠AOM和∠AOB的度数，然后两角相减即为∠BOM的度数
解答：
解；连接AO，
∵正三角形AMN与正五边形ABCDE内接于⊙O，
∴∠AOM=
×360°=120°，∴∠AOB=
×360°=72°，∵∠BOM=∠AOM-∠AOB，
∴∠BOM=120°-72°=48°
故答案为：48°
点评：本题主要考查正多边形和圆这一知识点，解答此题的关键是连接AO，由等弧所对的圆心角相等来解决问题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
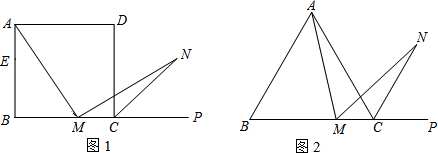
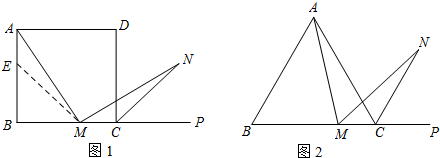N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
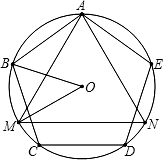如图，正三角形AMN与正五边形ABCDE内接于⊙O，则∠BOM的度数是