题目内容
【题目】某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本,并且所购买A笔记本的数量要不多于B笔记本数量的![]() ,但又不少于B笔记本数量
,但又不少于B笔记本数量![]() ,设买A笔记本n本,买两种笔记本的总费为w元.
,设买A笔记本n本,买两种笔记本的总费为w元.
(1)写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
(2)购买这两种笔记本各多少时,费用最少?最少的费用是多少元?
(3)商店为了促销,决定仅对A种类型的笔记本每本让利a元销售,B种类型笔记本售价不变.问购买这两种笔记本各多少本时花费最少?
【答案】(1)5≤n≤![]() ;(2)当n=5时,w取到最小值为260元;(3)当4﹣a>0,即a<4时,n=5,即买A笔记本5本,B笔记本25本,花费最少;当4﹣a=0,即a=4时,5≤n≤13,即买A笔记本5﹣13本,B笔记本25﹣17本,花费为240元;当4﹣a<0,即a>4时,n=13,即买A笔记本13本,B笔记本17本,花费最少.
;(2)当n=5时,w取到最小值为260元;(3)当4﹣a>0,即a<4时,n=5,即买A笔记本5本,B笔记本25本,花费最少;当4﹣a=0,即a=4时,5≤n≤13,即买A笔记本5﹣13本,B笔记本25﹣17本,花费为240元;当4﹣a<0,即a>4时,n=13,即买A笔记本13本,B笔记本17本,花费最少.
【解析】
(1)根据题意得到w(元)关于n(本)的函数关系式,可得到一个关于n的不等式组,可求出n的取值范围,再结合花费的函数式,可求出x的具体数值;
(2)结合花费的函数式,可求出x的具体数值;
(3)根据a的取值范围即可得到结论.
解:(1)由题意可知:w=12n+8(30﹣n),
∴w=4n+240,
又∵A笔记本的数量要不多于B笔记本数量的![]() ,但又不少于B笔记本数量的
,但又不少于B笔记本数量的![]() .
.
∴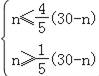 ,解得5≤n≤
,解得5≤n≤![]() ,
,
(2)w=4n+240,
∵k=4>0,
∴w随n的增大而增大,
∴当n=5时,w取到最小值为260元.
(3)w=(12﹣a)n+8(30﹣n),
∴w=(4﹣a)n+240,
当4﹣a>0,即a<4时,n=5,即买A笔记本5本,B笔记本25本,花费最少,
当4﹣a=0,即a=4时,5≤n≤13,即买A笔记本5﹣13本,B笔记本25﹣17本,花费为240元,
当4﹣a<0,即a>4时,n=13,即买A笔记本13本,B笔记本17本,花费最少.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案