题目内容
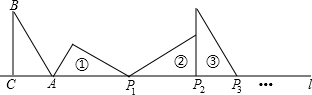
如图：在△ABC中，∠ACB=90°，∠B=30°，AC=1，AC在直线l上，将△ABC绕点A顺时针旋转到位置①，可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=2+
；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，可得到点P3，此时AP3=3+
；…，按此规律继续旋转，直到得到点P2014为止，则AP2014=（ ）
| 3 |
| 3 |
A、2012+671
| ||
B、2013+671
| ||
C、2014+671
| ||
D、2015+671
|
练习册系列答案
开心蛙口算题卡系列答案
相关题目
实数-17的相反数是（ ）
| A、17 | ||
B、
| ||
| C、-17 | ||
D、-
|
已知无理数1+
，若a＜1+
＜b，其中a、b为两个连续的整数，则ab的值为（ ）
| 3 |
| 3 |
| A、2 | B、6 | C、12 | D、20 |
下列运算正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如果m是任意实数，则点P（m，1-2m）一定不在（ ）
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |
如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0），（4，0）．根据这个规律探索可得，第100个点的坐标为（ ）| A、（14，8） | B、（13，0） | C、（100，99） | D、（15，14） |
如图，在直角坐标系中，已知点A（-3，0），B（0，4）对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…则△2012的直角顶点的坐标为（ ）
| A、（8052，0） | ||||
| B、（8040，0） | ||||
C、（8032+
| ||||
D、（8044+
|
