题目内容
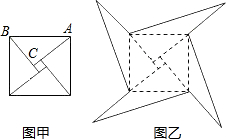 图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,面积为74的正方形.在Rt△ABC中,若直角边BC=5,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到图乙所示的“数学风车”.
图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,面积为74的正方形.在Rt△ABC中,若直角边BC=5,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到图乙所示的“数学风车”.(1)这个风车至少需要绕着中心旋转
(2)求这个风车的外围周长(图乙中的实线).
分析:(1)根据旋转角及旋转对称图形的定义结合图形特点作答.
(2)在直角△ABC中,已知BC,AB,根据勾股定理即可计算AC的长,AC=7,故求得BD即可计算风车的外围周长.
(2)在直角△ABC中,已知BC,AB,根据勾股定理即可计算AC的长,AC=7,故求得BD即可计算风车的外围周长.
解答:解:(1):∵360°÷4=90°,
∴该图形绕中心至少旋转90度后能和原来的图案互相重合.
(2)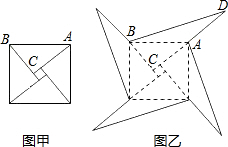
在直角△BCD中,BD为斜边,
已知BC=5,AB=
,
由勾股定理得:AC=7,CD=7+5=12,
∴BD=
=13,
∵风车的外围周长为4(BD+AD)=4(13+5)=72.
∴该图形绕中心至少旋转90度后能和原来的图案互相重合.
(2)

在直角△BCD中,BD为斜边,
已知BC=5,AB=
| 74 |
由勾股定理得:AC=7,CD=7+5=12,
∴BD=
| 52+122 |
∵风车的外围周长为4(BD+AD)=4(13+5)=72.
点评:本题考查了旋转角的定义及勾股定理在直角三角形中的运用,考查了全等三角形对应边相等的性质,本题中正确的计算BD是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 9、图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在 Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是( )
9、图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在 Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是( ) 图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=6,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是
图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=6,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是
