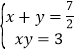题目内容
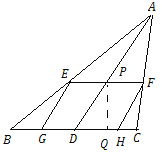
【题目】在△ABC中,已知BC=6,BC边上中线AD=5.点P为线段AD上一点(与点A、D不重合),过P点作EF∥BC,分别交边AB、AC于点E、F,过点E、F分别作EG∥AD,FH∥AD,交BC边于点G、H.
(1)求证:P是线段EF的中点;
(2)当四边形EGHF为菱形时,求EF的长;
(3) 如果sin∠ADC=![]() ,设AP长为x,四边形EGHF面积为y,求y关于x的函数解析式及其定义域.
,设AP长为x,四边形EGHF面积为y,求y关于x的函数解析式及其定义域.
【答案】(1)证明见解析;(2)![]() ;(3)y=-x2+5x(0<x<5)
;(3)y=-x2+5x(0<x<5)
【解析】
试题(1)利用EF∥BC,得出△AEP∽△ABD,△AFP∽△ACD,得出![]() ,又BD=CD,则得出结论;(2)由EF∥BC,得出△AEF∽△ABC,得出
,又BD=CD,则得出结论;(2)由EF∥BC,得出△AEF∽△ABC,得出![]() (相似三角形对应中线的比等于对应边的比),则可求出EF;(3)过点P作PQ⊥BC于Q,易知四边形EGHF是平行四边形,根据S四边形EGHF=GH×PQ=EF×PQ=y,利用△AEF∽△ABC,求得EF,利用sin∠ADC=
(相似三角形对应中线的比等于对应边的比),则可求出EF;(3)过点P作PQ⊥BC于Q,易知四边形EGHF是平行四边形,根据S四边形EGHF=GH×PQ=EF×PQ=y,利用△AEF∽△ABC,求得EF,利用sin∠ADC=![]() 求得PQ,则可得y关于x的关系式.
求得PQ,则可得y关于x的关系式.
解:(1)∵EF∥BC,∴△AEP∽△ABD,△AFP∽△ACD,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
又∵BD=CD,∴EP=FP,即P是EF中点.
(2)∵EF∥BC,∴△AEF∽△ABC,
∴![]() ,
,
设EF=a,则EG=EF=a,
∵EG∥AD,EF∥BC,∴四边形EGDP是平行四边形,
∴PD=EG=a,∴AP=AD-PD=5-a,∴![]() ,解得
,解得![]() ,即EF=
,即EF=![]() .
.
(3)如图,过点P作PQ⊥BC于Q,
∵△AEF∽△ABC,∴![]() ,即
,即![]() ,解得EF=
,解得EF=![]() .
.
∵sin∠ADC=![]() =
=![]() ,∴PQ=
,∴PQ=![]() ×PD=
×PD=![]() (5-x).
(5-x).
∵EG∥AD,FH∥AD,∴EG∥FH,又∵EF∥BC,
∴四边形EGHF是平行四边形.
∴GH=EF,
∴S四边形EGHF=GH×PQ=EF×PQ=y=![]() ×
×![]() (5-x)=-x2+5x,
(5-x)=-x2+5x,
其中0<x<5.