题目内容
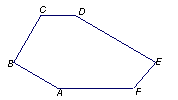
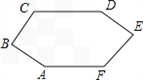
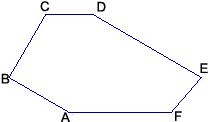 28、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.
28、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.分析:通过分析条件可知,连接AD,构造四边形ABCD,利用内角和求出∠BAD+∠ADC=150°,再利用四边形ADEF中的内角和关系求出∠F=130°.
解答: 解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
∵AB⊥BC,
∴∠B=90°.
又∵∠C=120°,
∴∠BAD+∠ADC=150°.
∵CD∥AF,
∴∠CDA=∠DAF.
在四边形ADEF中,
∠DAF+∠EDA+∠F+∠E=360°,
∴∠F+∠E=210°.
又∵∠E=80°,
∴∠F=130°.
 解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.∵AB⊥BC,
∴∠B=90°.
又∵∠C=120°,
∴∠BAD+∠ADC=150°.
∵CD∥AF,
∴∠CDA=∠DAF.
在四边形ADEF中,
∠DAF+∠EDA+∠F+∠E=360°,
∴∠F+∠E=210°.
又∵∠E=80°,
∴∠F=130°.
点评:主要考查了四边形的内角和是360度的实际运用.
解题关键是构造四边形利用已知条件结合四边形内角和求解.
解题关键是构造四边形利用已知条件结合四边形内角和求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
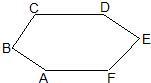 29、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.
29、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.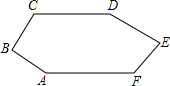 (2013•河西区一模)如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,则∠F=
(2013•河西区一模)如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,则∠F=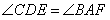 ,
,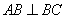 ,
,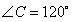 ,
,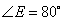 ,试求
,试求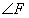 的度数.
的度数.