题目内容
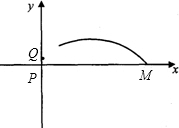 (1)在足球比赛中,当守门员远离球门时,进攻队员常常使用“吊射”的战术(把球高高地挑过守门员的头顶射入球门).一位球员在离对方球门30米的M处起脚吊射,假如球飞行的路线是一条抛物线,在离球门14米时,足球到达最大高度
(1)在足球比赛中,当守门员远离球门时,进攻队员常常使用“吊射”的战术(把球高高地挑过守门员的头顶射入球门).一位球员在离对方球门30米的M处起脚吊射,假如球飞行的路线是一条抛物线,在离球门14米时,足球到达最大高度| 32 | 3 |
(2)在(1)中,若守门员站在距球门2米远处,而守门员跳起后最多能摸到2.75米高处,他能否在空中截住这次吊射?
分析:(1)先求出抛物线的解析式,再根据抛物线的解析式判断球是否会进入球门;
(2)根据抛物线的解析式求出当x=2时,求所处的位置,便可判断守门员不能在空中截住这次吊射.
(2)根据抛物线的解析式求出当x=2时,求所处的位置,便可判断守门员不能在空中截住这次吊射.
解答:解:(1)由题意可知,抛物线的顶点(14,
),
抛物线过点M(30,0),
设它的解析式为y=a(x-14)2+
,
把点M(30,0)代入y=a(x-14)2+
,
解得a=-
,
∴抛物线的解析式为y=-
(x-14)2+
,
令x=0,得y=
,即足球到达球门时的高度为
米,
>2.44,
∴球不会进入球门;
(2)y=-
(x-14)2+
,
令x=2,得y=
,
即球在离球门2米处得高度为
米,
>2.75,
∴守门员不能在空中截住这次吊射.
| 32 |
| 3 |
抛物线过点M(30,0),
设它的解析式为y=a(x-14)2+
| 32 |
| 3 |
把点M(30,0)代入y=a(x-14)2+
| 32 |
| 3 |
解得a=-
| 1 |
| 24 |
∴抛物线的解析式为y=-
| 1 |
| 24 |
| 32 |
| 3 |
令x=0,得y=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
∴球不会进入球门;
(2)y=-
| 1 |
| 24 |
| 32 |
| 3 |
令x=2,得y=
| 14 |
| 3 |
即球在离球门2米处得高度为
| 14 |
| 3 |
| 14 |
| 3 |
∴守门员不能在空中截住这次吊射.
点评:本题主要考查了二次函数的实际应用,解答二次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义,属于中档题.

练习册系列答案
相关题目
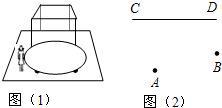 19、如图(1),在足球比赛中,球员射中球门的难易程度与他所处的位置的射门角度的大小有关.如果在一次比赛中,小华和小勇分别处在图(2)中的A,B两点,球门的位置在线段CD,如果球在小华的脚下,此时他应该选择传给小勇还是自己射门较好?(通过尺规作图说明原因)
19、如图(1),在足球比赛中,球员射中球门的难易程度与他所处的位置的射门角度的大小有关.如果在一次比赛中,小华和小勇分别处在图(2)中的A,B两点,球门的位置在线段CD,如果球在小华的脚下,此时他应该选择传给小勇还是自己射门较好?(通过尺规作图说明原因)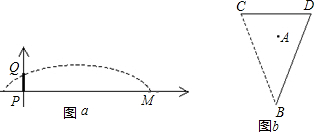
 10、如图,在足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同伴乙已经助攻冲到B点,此时甲是直接射门好,还是将球传给乙,由乙射门好?(仅从射门角度考虑)
10、如图,在足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同伴乙已经助攻冲到B点,此时甲是直接射门好,还是将球传给乙,由乙射门好?(仅从射门角度考虑)