题目内容
抛物线 的最低点坐标是________.
的最低点坐标是________.
(-1,-2)
分析:由于函数的二次项系数为正数,故开口向上,函数有最小值,配方后即可求出最低点坐标.
解答:原式可化为:y= (x2+2x)-
(x2+2x)-
= (x2+2x+1-1)-
(x2+2x+1-1)-
= (x+1)2-2
(x+1)2-2
则其最低点坐标为(-1,-2).
故答案为(-1,-2).
点评:本题考查了二次函数的最值,将一般式配方,利用顶点式是解答此题的最简、最有效方法.
分析:由于函数的二次项系数为正数,故开口向上,函数有最小值,配方后即可求出最低点坐标.
解答:原式可化为:y=
 (x2+2x)-
(x2+2x)-
=
 (x2+2x+1-1)-
(x2+2x+1-1)-
=
 (x+1)2-2
(x+1)2-2则其最低点坐标为(-1,-2).
故答案为(-1,-2).
点评:本题考查了二次函数的最值,将一般式配方,利用顶点式是解答此题的最简、最有效方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
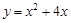 的最低点坐标是 .
的最低点坐标是 .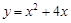 的最低点坐标是 .
的最低点坐标是 . 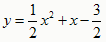 的最低点坐标是( ),当x( )时,y随x的增大而增大。
的最低点坐标是( ),当x( )时,y随x的增大而增大。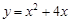 的最低点坐标是 .
的最低点坐标是 .